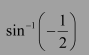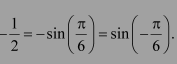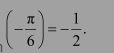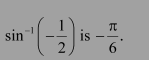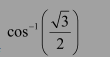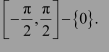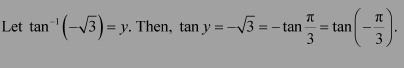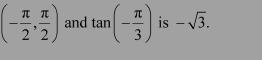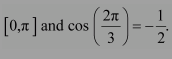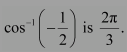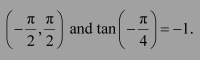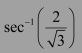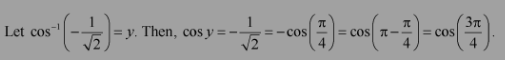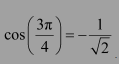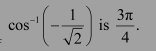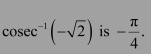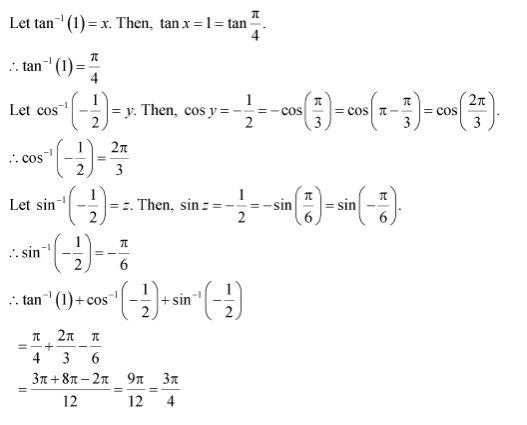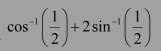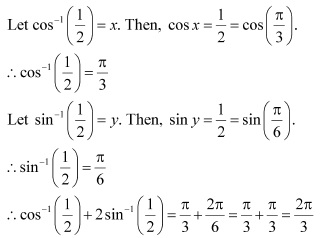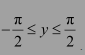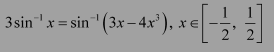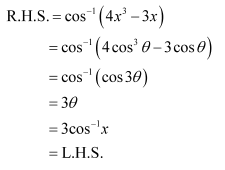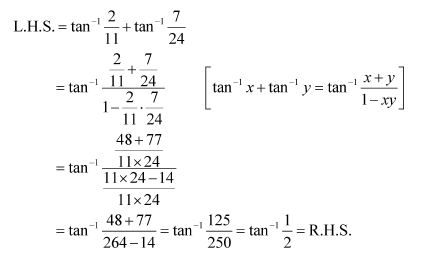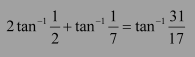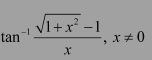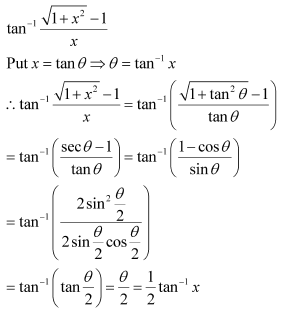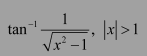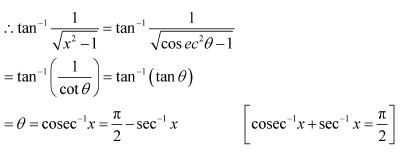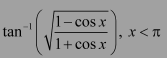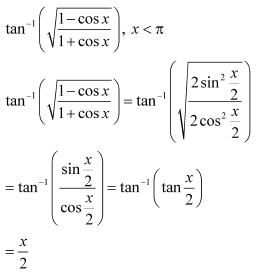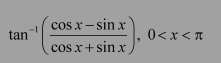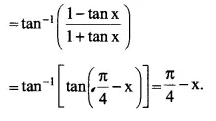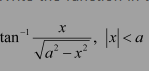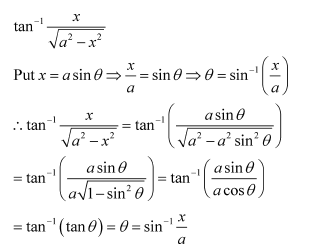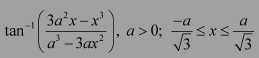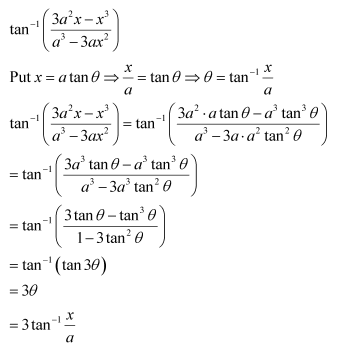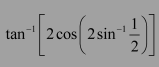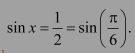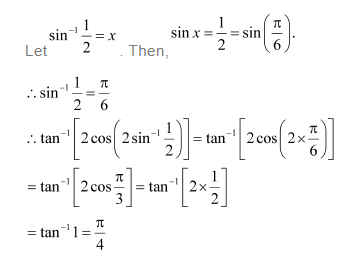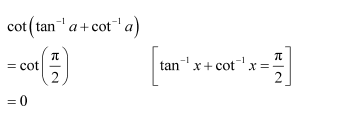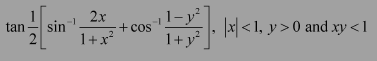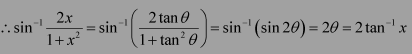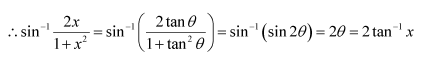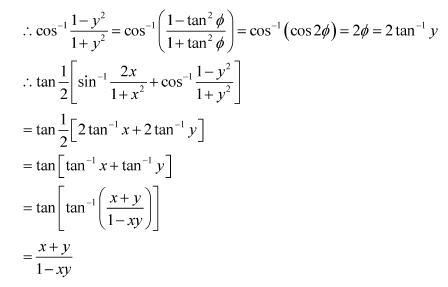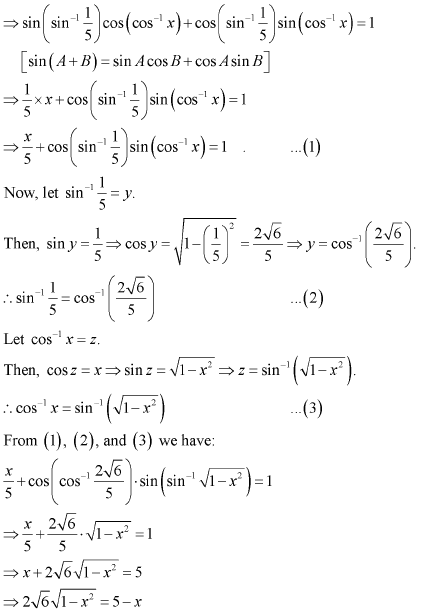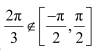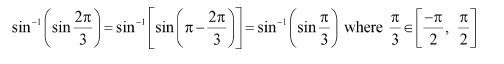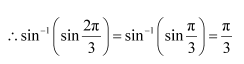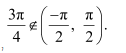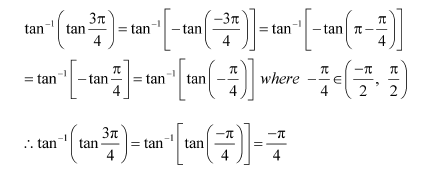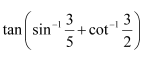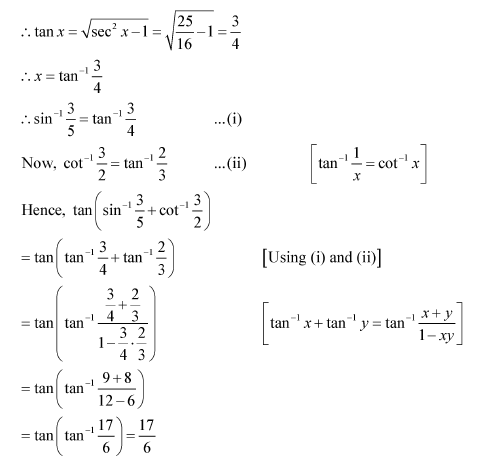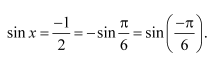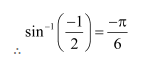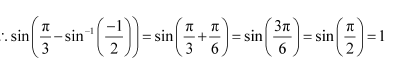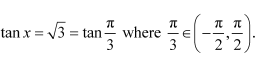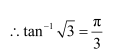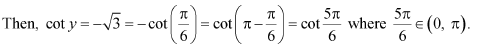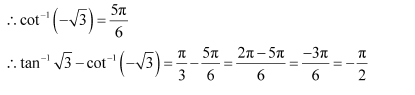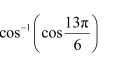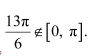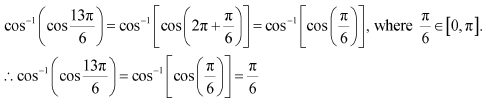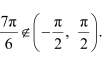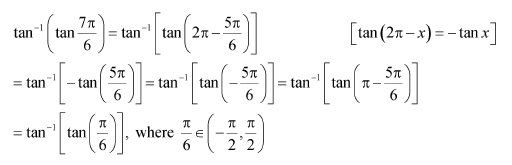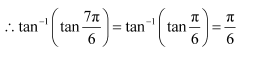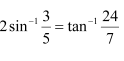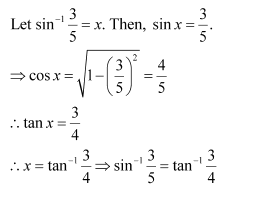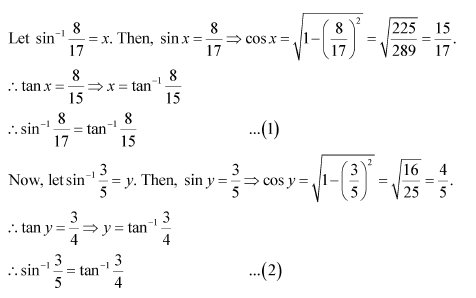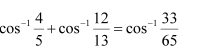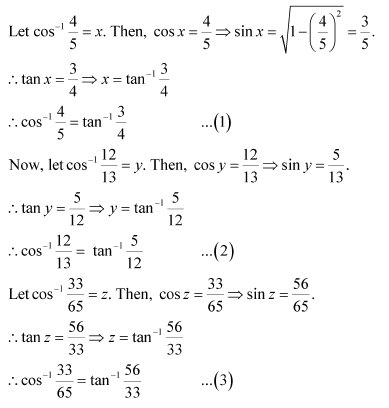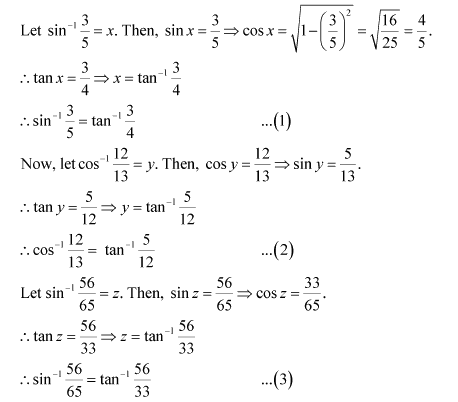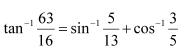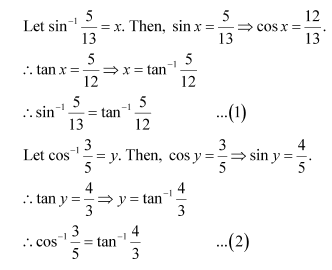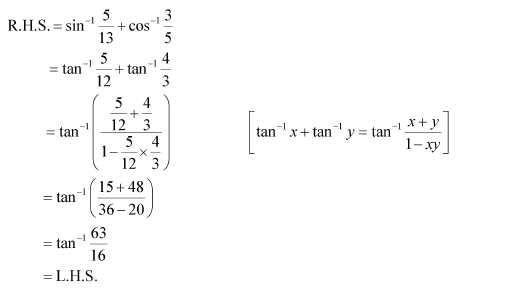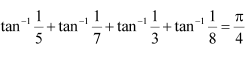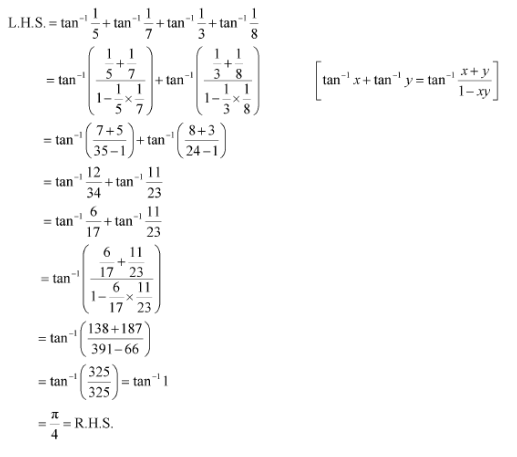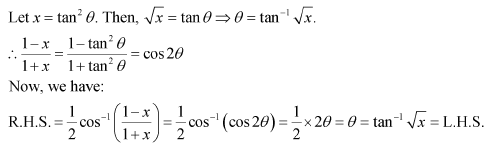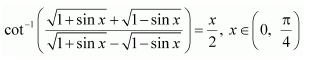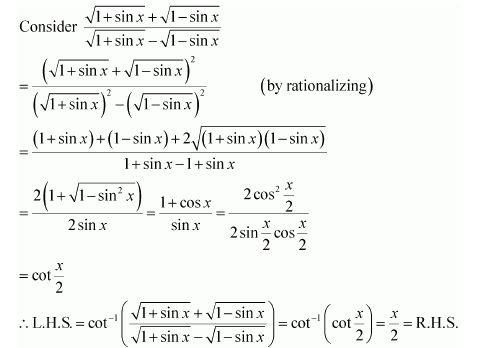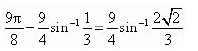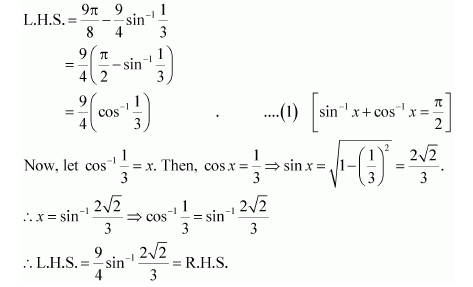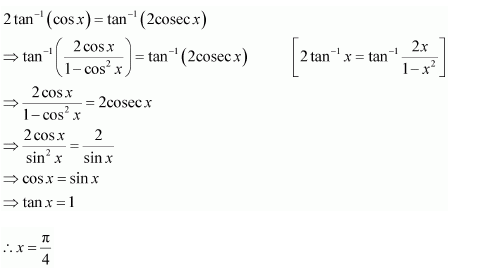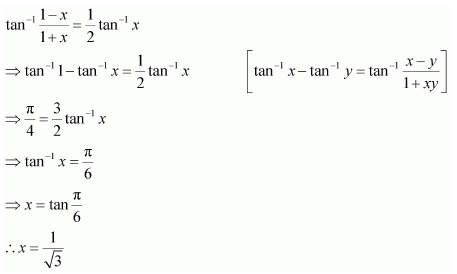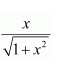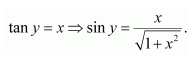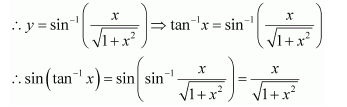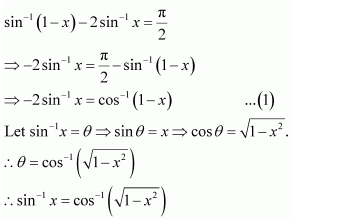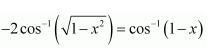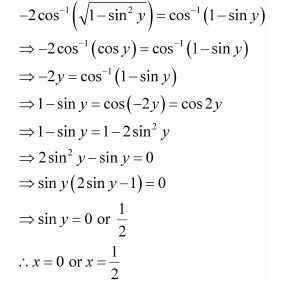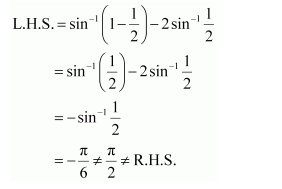Students can download NCERT Solutions For Class 12 Maths Chapter 2. Here, we Have given detailed explanations for every question in an easily understandable manner. Class 12 Maths NCERT Solutions plays a crucial role in the student’s preparation. We have covered all important topics in this article. Each topic is given with a brief explanation. Students can easily practice Class 12 Maths NCERT Book Solution. This article will clarify your doubts regarding all the questions which are related to NCERT Solutions For Class 12 Maths Chapter 2. You can complete your home assignments and prepare for exams by downloading Maths Chapter 2. NCERT Solutions For Class 12 Maths has been written for the students to get a high score in the exams. you can clarify your doubts regarding this chapter by simply downloading it.
NCERT Solutions Of Class 12 Maths Chapter 2 – Inverse Trigonometric Functions
| Name OF The Section | Topic Name |
| 2 | Inverse Trigonometric Functions |
| 2.1 | Introduction |
| 2.2 | Basic Concepts |
| 2.3 | Properties of Inverse Trigonometric Functions |
Class 12 Maths Chapter 2 NCERT Solutions – 2.1 Introduction
Question 1:
Find the principal value of
Answer:
Let sin-1 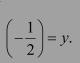
We know that the range of the principal value branch of sin−1 is
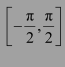
Therefore, the principal value of
Question 2:
Find the principal value of
Answer:
We know that the range of the principal value branch of cos−1 is
Therefore, the principal value of
Question 3:
Find the principal value of cosec−1 (2)
Answer:
Let cosec−1 (2) = y. Then,
We know that the range of the principal value branch of cosec−1 is
Therefore, the principal value of
Question 4:
Find the principal value of
Answer:
We know that the range of the principal value branch of tan−1 is
Therefore, the principal value of
Question 5:
Find the principal value of
Answer:
We know that the range of the principal value branch of cos−1 is
Therefore, the principal value of
Question 6:
Find the principal value of tan−1 (−1)
Answer:
Let tan−1 (−1) = y. Then,
We know that the range of the principal value branch of tan−1 is
Therefore, the principal value of
Question 7:
Find the principal value of
Answer:
We know that the range of the principal value branch of sec−1 is
Therefore, the principal value of
Question 8:
Find the principal value of
Answer:
We know that the range of the principal value branch of cot−1 is (0,π) and
Therefore, the principal value of
Question 9:
Find the principal value of
Answer:
We know that the range of the principal value branch of cos−1 is [0,π] and
Therefore, the principal value of
Question 10:
Find the principal value of
Answer:
We know that the range of the principal value branch of cosec−1 is
Therefore, the principal value of
Question 11:
Find the value of
Answer:
Question 12:
Find the value of
Answer:
Question 13:
Find the value of if sin−1 x = y, then
(A) (B)
(C) (D)
Answer:
It is given that sin−1 x = y.
We know that the range of the principal value branch of sin−1 is
Therefore,
Question 14:
Find the value of is equal to
(A) π (B) (C)
(D)
Answer:
NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions – Exercise 2.2
Question 1:
Prove
Answer:
To prove,
Let x = sinθ. Then,
We have,
R.H.S. =
= 3θ
= L.H.S.
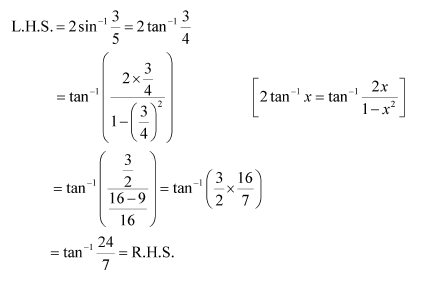
Question 2:
Prove
Answer:
To prove:
Let x = cosθ. Then, cos−1 x =θ.
We have,
Question 3:
Prove
Answer:
To prove:
Question 4:
Prove
Answer:
To prove:
Question 5:
Write the function in the simplest form:
Answer:
Question 6:
Write the function in the simplest form:
Answer:
Put x = cosec θ ⇒ θ = cosec−1 x
Question 7:
Write the function in the simplest form:
Answer:
Question 8:
Write the function in the simplest form:
Answer:
Dividing numerator and denominator by cos x
Question 9:
Write the function in the simplest form:
Answer:
Question 10:
Write the function in the simplest form:
Answer:
Question 11:
Find the value of
Answer:
Let Then,
Question 12:
Find the value of
Answer:
Question 13:
Find the value of
Answer:
Let x = tan θ. Then, θ = tan−1 x.
Let y = tan Φ. Then, Φ = tan−1 y.
Let y = tan Φ. Then, Φ = tan−1 y.
Question 14:
If 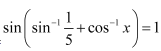
Answer:
On squaring both sides, we get:
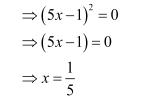
Question 15:
If 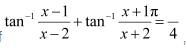
Answer:
Hence, the value of x is
Question 16:
Find the values of
Answer:
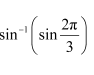
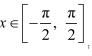
Here,
Now, 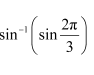
Question 17:
Find the values of
Answer:
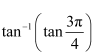
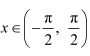
Here
Now, 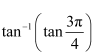
Question 18:
Find the values of
Answer:
Let Then,
Question 19:
Find the values of 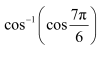
(A) (B)
(C)
(D)
Answer:
We know that cos−1 (cos x) = x if which is the principal value branch of cos −1x.
Here,
Now, 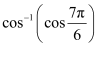
cos-1cos7π6 = cos-1cosπ+π6cos-1cos7π6 = cos-1- cosπ6 as, cosπ+θ = – cos θcos-1cos7π6 = cos-1- cosπ-5π6cos-1cos7π6 = cos-1– cos 5π6 as, cosπ-θ = – cos θ
The correct answer is B.
Question 20:
Find the values of 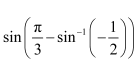
(A) (B)
(c)
(D) 1
Answer:
Let Then,
We know that the range of the principal value branch of
The correct answer is D.
Question 21:
Find the values of 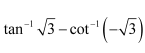
(A) π (B) (C)0 (D)
Answer:
Let, Then,
We know that the range of the principal value branch of
Let
The range of the principal value branch of
The correct answer is B.
NCERT Solutions Class 12 Maths Chapter 2 Inverse Trigonometric Functions – Miscellaneous Solutions
Question 1:
Find the value of
Answer:
We know that cos−1 (cos x) = x if 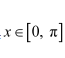
Here,
Now, 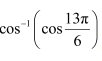
Question 2:
Find the value of
Answer:
We know that tan−1 (tan x) = x if 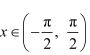
Here,
Now,

Question 3:
Prove
Answer:
Now, we have:
Question 4:
Prove
Answer:
Now, we have:
Question 5:
Prove
Answer:
Now, we will prove that:
Question 6:
Prove
Answer:
Now, we have:
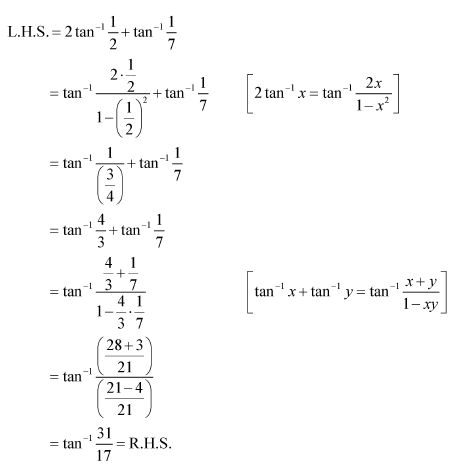
Question 7:
Prove
Answer:
Using (1) and (2), we have
Question 8:
Prove
Answer:
Question 9:
Prove
Answer:
Question 10:
Prove
Answer:
Question 11:
Prove 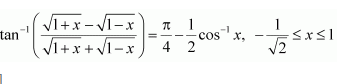
Question 12:
Prove
Answer:
Question 13:
Solve
Answer:
Question 14:
Solve
Answer:
Question 15:
Solve 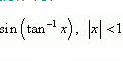
(A) 
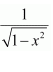
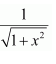
Answer:
Let tan−1x = y. Then,
The correct answer is D.
Question 16:
Solve , then x is equal to
(A) (B)
(C) 0 (D)
Answer:
Therefore, from equation (1), we have
Put x = sin y. Then, we have:
But, when
it can be observed that:
∴is not the solution of the given equation.
Thus, x = 0.
Hence, the correct answer is C.
Question 17:
Solve 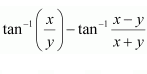
(A) (B)
(C)
(D)
Answer:
Hence, the correct answer is C.