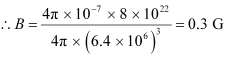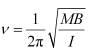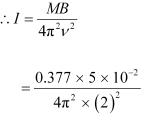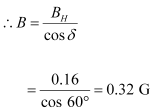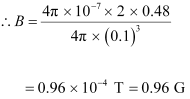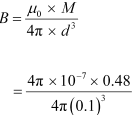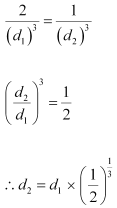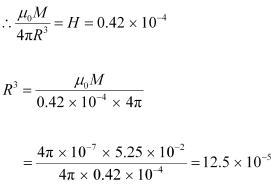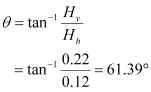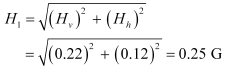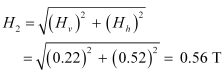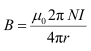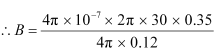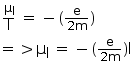NCERT Solutions For Class 12 Physics Chapter 5 are provided in this article. Discovery of magnetism, the magnetic field lines, equivalent solenoid to a bar magnet, the electrostatic analog, and Gauss law are introduced in this unit. Class 12 Physics NCERT Chapter 5 Solutions will be very useful for students who are looking to make their foundations strong from the basics. Solving exercise problems given at the end of the unit in all NCERT Solutions For Class 12 Physics will enable the students to think in ways that are useful in practical applications, and put those theoretical concepts to good use. Physics NCERT Solutions Class 12 Chapter 5 which is provided in this article can remove the obstacles if you ever got stuck on a problem.
Class 12 Physics NCERT Chapter 5 Solutions
Topic-wise overview of NCERT Solutions For Class 12 Physics Chapter 5 is provided in the following table.
| Section | Topic |
| 5 | Magnetism and Matter |
| 5.1 | Introduction |
| 5.2 | The Bar Magnet |
| 5.3 | Magnetism and Gauss’s Law |
| 5.4 | The Earth’s Magnetism |
| 5.5 | Magnetization and Magnetic Intensity |
| 5.6 | Magnetic Properties of Materials |
| 5.7 | Permanent Magnets and Electromagnets |
Physics NCERT Solutions Class 12 Chapter 5:
Question 5.1:
Answer the following questions regarding earth’s magnetism:
(a) A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.
(b) The angle of dip at a location in southern India is about 18º.
Would you expect a greater or smaller dip angle in Britain?
(c) If you made a map of magnetic field lines at Melbourne in Australia, would the lines seem to go into the ground or come out of the ground?
(d) In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic north or south pole?
(e) The earth’s field, it is claimed, roughly approximates the field due to a dipole of the magnetic moment 8 × 1022 J T−1 located at its center. Check the order of magnitude of this number in some way.
(f ) Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all?
Solution:
(a) The three independent quantities conventionally used for specifying the earth’s magnetic field are:
(i) Magnetic declination,
(ii) Angle of dip, and
(iii) Horizontal component of earth’s magnetic field
(b)The angle of dip at a point depends on how far the point is located with respect to the North Pole or the South Pole. The angle of dip would be greater in Britain (it is about 70°) than in southern India because the location of Britain on the globe is closer to the magnetic North Pole.
(c) It is hypothetically considered that a huge bar magnet is dipped inside the earth with its north pole near the geographic South Pole and its south pole near the geographic North Pole.
Magnetic field lines emanate from a magnetic north pole and terminate at a magnetic south pole. Hence, in a map depicting the earth’s magnetic field lines, the field lines at Melbourne, Australia would seem to come out of the ground.
(d) If a compass is located on the geomagnetic North Pole or the South Pole, then the compass will be free to move in the horizontal plane while the earth’s field is exactly vertical to the magnetic poles. In such a case, the compass can point in any direction.
(e) Magnetic moment, M = 8 × 1022 J T−1
The radius of the earth, r = 6.4 × 106 m
Magnetic field strength,
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
This quantity is of the order of magnitude of the observed field on earth.
(f)Yes, there are several local poles on the earth’s surface oriented in different directions. A magnetized mineral deposit is an example of a local N-S pole.
Question 5.2:
Answer the following questions:
(a) The earth’s magnetic field varies from point to point in space.
Does it also change with time? If so, on what time scale does it change appreciably?
(b) The earth’s core is known to contain iron. Yet geologists do not regard this as a source of the earth’s magnetism. Why?
(c) The charged currents in the outer conducting regions of the earth’s core are thought to be responsible for the earth’s magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?
(d) The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth’s field in such a distant past?
(e) The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?
(f ) Interstellar space has an extremely weak magnetic field of the order of 10−12 T. Can such a weak field be of any significant consequence? Explain.
[Note: Exercise 5.2 is meant mainly to arouse your curiosity. Answers to some questions above are tentative or unknown. Brief answers wherever possible are given at the end. For details, you should consult a good text on geomagnetism.]Solution:
(a) Earth’s magnetic field changes with time. It takes a few hundred years to change by an appreciable amount. The variation in the earth’s magnetic field with time cannot be neglected.
(b)Earth’s core contains molten iron. This form of iron is not ferromagnetic. Hence, this is not considered a source of earth’s magnetism.
(c)The radioactivity in the earth’s interior is the source of energy that sustains the currents in the outer conducting regions of the earth’s core. These charged currents are considered to be responsible for the earth’s magnetism.
(d)Earth reversed the direction of its field several times during its history of 4 to 5 billion years. These magnetic fields got weakly recorded in rocks during their solidification. One can get clues about the geomagnetic history from the analysis of this rock magnetism.
(e)Earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km) because of the presence of the ionosphere. In this region, the earth’s field gets modified because of the field of single ions. While in motion, these ions produce the magnetic field associated with them.
(f)An extremely weak magnetic field can bend charged particles moving in a circle. This may not be noticeable for a large radius path. With reference to the gigantic interstellar space, the deflection can affect the passage of charged particles.
Question 5.3:
A short bar magnet placed with its axis at 30º with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 × 10−2 J. What is the magnitude of the magnetic moment of the magnet?
Solution:
Magnetic field strength, B = 0.25 T
Torque on the bar magnet, T = 4.5 × 10−2 J
The angle between the bar magnet and the external magnetic field,θ = 30°
Torque is related to magnetic moment (M) as:
T = MB sin θ
M = T/Sinθ
Hence, the magnetic moment of the magnet is 0.36 J T−1.
Question 5.4:
A short bar magnet of magnetic moment m = 0.32 J T−1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Solution:
Moment of the bar magnet, M = 0.32 J T−1
External magnetic field, B = 0.15 T
(a)The bar magnet is aligned along the magnetic field. This system is considered as being in stable equilibrium. Hence, the angle θ, between the bar magnet and the magnetic field is 0°.
Potential energy of the system = – MB cosθ
(b)The bar magnet is oriented 180° to the magnetic field. Hence, it is in unstable equilibrium.
θ = 180°
Potential energy = − MB cos θ
= -0.32 x 0.15 cos180°
= 4.8 x 10-2 J
Question 5.5:
A closely wound solenoid of 800 turns and area of cross-section 2.5 × 10−4 m2 carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
Solution:
Number of turns in the solenoid, n = 800
Area of cross-section, A = 2.5 × 10−4 m2
Current in the solenoid, I = 3.0 A
A current-carrying solenoid behaves like a bar magnet because a magnetic field develops along its axis, i.e., along its length.
The magnetic moment associated with the given current-carrying solenoid is calculated as:
M = n I A
= 800 × 3 × 2.5 × 10−4
= 0.6 J T−1
Question 5.6:
If the solenoid in Exercise 5.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of the torque on the solenoid when its axis makes an angle of 30° with the direction of applied field?
Solution:
Magnetic field strength, B = 0.25 T
Magnetic moment, M = 0.6 T−1
The angle θ, between the axis of the solenoid and the direction of the applied field, is 30°. Therefore, the torque acting on the solenoid is given as:
τ = MB Sinθ
= 0.6 x 0.25 Sin 30°
= 7.5 x 10-2 J
Question 5.7:
A bar magnet of magnetic moment 1.5 J T−1 lies aligned with the direction of a uniform magnetic field of 0.22 T.
(a) What is the amount of work required by an external torque to turn the magnet to align its magnetic moment: (i) normal to the field direction, (ii) opposite to the field direction?
(b) What is the torque on the magnet in cases (i) and (ii)?
Solution:
(a)Magnetic moment, M = 1.5 J T−1
Magnetic field strength, B = 0.22 T
(i)Initial angle between the axis and the magnetic field, θ1 = 0°
The final angle between the axis and the magnetic field, θ2 = 90°
The work required to make the magnetic moment normal to the direction of the magnetic field is given as:
W = -MB (cosθ2 – cosθ1)
= -1.5 x 0.22(cos 90° – cos 0°)
= -0.33(0 – 1)
= 0.33 J
(ii) Initial angle between the axis and the magnetic field, θ1 = 0°
The final angle between the axis and the magnetic field, θ2 = 180°
The work required to make the magnetic moment opposite to the direction of the magnetic field is given as:
W = -MB (cosθ2 – cosθ1)
= -1.5 x 0.22(cos 180° – cos 0°)
= -0.33(-1 – 1)
= 0.66 J
(b) For case (i): θ = θ2 = 90°
∴ Torque, τ = MB Sinθ
= 1.5 x 0.22Sin 90°
= 0.33 J
For case (ii): θ = θ2 = 180°
∴ Torque, τ = MB Sinθ
= MB Sin 180° = 0 J
Question 5.8:
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10−4 m2, carrying a current of 4.0 A, is suspended through its center allowing it to turn in a horizontal plane.
(a) What is the magnetic moment associated with the solenoid?
(b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10−2 T is set up at an angle of 30º with the axis of the solenoid?
Solution:
Number of turns on the solenoid, n = 2000
Area of the cross-section of the solenoid, A = 1.6 × 10−4 m2
Current in the solenoid, I = 4 A
(a)The magnetic moment along the axis of the solenoid is calculated as:
M = nAI
= 2000 × 1.6 × 10−4 × 4
= 1.28 Am2
(b)Magnetic field, B = 7.5 × 10−2 T
The angle between the magnetic field and the axis of the solenoid, θ = 30°
Torque, τ = MB Sinθ
= 1.28 x 7.5 x 10-2 sin 30°
= 4.8 x 10-2 Nm
Since the magnetic field is uniform, the force on the solenoid is zero. The torque on the solenoid is 4.8 x 10-2 Nm
Question 5.9:
A circular coil of 16 turns a and radius of 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 × 10−2 T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s−1. What is the moment of inertia of the coil about its axis of rotation?
Solution:
Number of turns in the circular coil, N = 16
Radius of the coil, r = 10 cm = 0.1 m
Cross-section of the coil, A = πr2 = π × (0.1)2 m2
Current in the coil, I = 0.75 A
Magnetic field strength, B = 5.0 × 10−2 T
Frequency of oscillations of the coil, v = 2.0 s−1
∴Magnetic moment, M = NIA = NIπr²
= 16 × 0.75 × π × (0.1)2
= 0.377 J T−1
Frequency is given by the relation:
Where,
I = Moment of Inertia of the coil
= 1.19 x 10-4 kg m2
Hence, the moment of inertia of the coil about its axis of rotation is 1.19 x 10-4 kg m2.
Question 5.10:
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 22º with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Solution:
The horizontal component of the earth’s magnetic field, BH = 0.35 G
Angle made by the needle with the horizontal plane = Angle of dip = δ = 22°
Earth’s magnetic field strength = B
We can relate B and BH as:
BH = B cosθ
∴ B = BH /cos δ
Hence, the strength of the earth’s magnetic field at the given location is 0.377 G.
Question 5.11:
At a certain location in Africa, a compass points 12º west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points 60º above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Solution:
The angle of declination,θ = 12°
The angle of dip, δ = 60°
The horizontal component of the earth’s magnetic field, BH = 0.16 G
Earth’s magnetic field at the given location = B
We can relate B and BH as:
BH = B cosδ
Earth’s magnetic field lines in the vertical plane, 12° West of the geographic meridian, making an angle of 60° (upward) with the horizontal direction. Its magnitude is 0.32 G.
Question 5.12:
A short bar magnet has a magnetic moment of 0.48 J T−1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the center of the magnet on (a) the axis, and (b) the equatorial lines (normal bisector) of the magnet.
Solution:
Magnetic moment of the bar magnet, M = 0.48 J T−1
(a) Distance, d = 10 cm = 0.1 m
The magnetic field at distance d, from the center of the magnet on the axis, is given by the relation:
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
The magnetic field is along with the S − N direction.
(b) The magnetic field at a distance of 10 cm (i.e., d = 0.1 m) on the equatorial line of the magnet is given as:
= 0.48 G
The magnetic field is along with the N − S direction.
Question 5.13:
A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north-south direction. Null points are found on the axis of the magnet at 14 cm from the center of the magnet. The earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null−point (i.e., 14 cm) from the center of the magnet? (At null points, the field due to a magnet is equal and opposite to the horizontal component of the earth’s magnetic field.)
Solution:
Earth’s magnetic field at the given place, H = 0.36 G
The magnetic field at a distance d, on the axis of the magnet, is given as:
…….. (i)
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
M= Magnetic Moment
The magnetic field at the same distance d, on the equatorial line of the magnet is given as:[Using Equation (i)]
Total magnetic field, B = B1 + B2
= H + H/2
= 0.36 + 0.18 = 0.54 G
Hence, the magnetic field is 0.54 G in the direction of the earth’s magnetic field.
Question 5.14:
If the bar magnet in exercise 5.13 is turned around by 180º, where will the new null points be located?
Solution:
The magnetic field on the axis of the magnet at a distance d1 = 14 cm, can be written as:
… (1)
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
H = Horizontal component of the magnetic field at d1
If the bar magnet is turned through 180°, then the neutral point will lie on the equatorial line.
Hence, the magnetic field at a distance d2, on the equatorial line of the magnet can be written as:
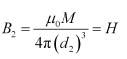
Equating equations (1) and (2), we get:
= 14 x 0.794 = 11.1 cm
The new null points will be located 11.1 cm on the normal bisector.
Question 5.15:
A short bar magnet of magnetic moment 5.25 × 10−2 J T−1 is placed with its axis perpendicular to the earth’s field direction. At what distance from the center of the magnet, the resultant field is inclined at 45º with the earth’s field on
(a) its normal bisector and (b) its axis. The magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Solution:
The magnetic moment of the bar magnet, M = 5.25 × 10−2 J T−1
The magnitude of the earth’s magnetic field at a place, H = 0.42 G = 0.42 × 10−4 T
(a) The magnetic field at a distance R from the center of the magnet on the normal bisector is given by the relation:
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
When the resultant field is inclined at 45° with the earth’s field, B = H
∴ R = 0.05 m = 5 cm
(b) The magnetic field at a distanced R’ from the center of the magnet on its axis is given as:
The resultant field is inclined at 45° with earth’s field.
∴ B’ = H
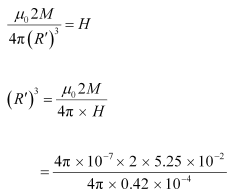
∴ R’ = 0.063 m = 6.3 cm
Question 5.16:
Answer the following questions:
(a) Why does a paramagnetic sample display greater magnetization (for the same magnetizing field) when cooled?
(b) Why is diamagnetism, in contrast, almost independent of temperature?
(c) If a toroid uses bismuth for its core, will the field in the core be (slightly) greater or (slightly) less than when the core is empty?
(d) Is the permeability of a ferromagnetic material independent of the magnetic field? If not, is it more for lower or higher fields?
(e) Magnetic field lines are always nearly normal to the surface of a ferromagnet at every point. (This fact is analogous to the static electric field lines being normal to the surface of a conductor at every point.) Why?
(f ) Would the maximum possible magnetization of a paramagnetic sample be of the same order of magnitude as the magnetization of a ferromagnet?
Solution:
(a) Owing to the random thermal motion of the molecules, the alignments of dipoles get disrupted at high temperatures. On cooling, this disruption is reduced. Hence, a paramagnetic sample displays greater magnetization when cooled.
(b) Each molecule of the diamagnetic material is not a magnetic dipole in itself. Hence, the random thermal motion of the molecules of the diamagnetic material (which is related to the temperature) does not affect the diamagnetism of the material.
(c) Bismuth is a diamagnetic substance. Hence, a toroid with a bismuth core has a magnetic field slightly less than a toroid whose core is empty.
(d) The permeability of ferromagnetic materials is not independent of the applied magnetic field. It is greater for a lower field.
(e) The permeability of a ferromagnetic material is always greater than one. Hence, magnetic field lines are always nearly normal to the surface of such materials at every point. The proof of this fact is based on the boundary conditions of the magnetic fields at the interface of two media.
(f) Yes, the maximum possible magnetization of a paramagnetic sample will be of the same order of magnitude as the magnetization of a ferromagnet. This requires high magnetizing fields for saturation.
Question 5.17:
Answer the following questions:
(a) Explain qualitatively based on the domain picture the irreversibility in the magnetization curve of a ferromagnet.
(b) The hysteresis loop of a soft iron piece has a much smaller area than that of a carbon steel piece. If the material is to go through repeated cycles of magnetization, which piece will dissipate greater heat energy?
(c) ‘A system displaying a hysteresis loop such as a ferromagnet, is a device for storing memory?’ Explain the meaning of this statement.
(d) What kind of ferromagnetic material is used for coating magnetic tapes in a cassette player, or building ‘memory stores’ in a modern computer?
(e) A certain region of space is to be shielded from magnetic fields.
Suggest a method.
Solution:
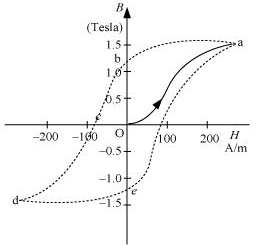
The hysteresis curve (B–H curve) of a ferromagnetic material is shown in the following figure.
a) It can be observed from the given curve that magnetization persists even when the external field is removed. This reflects the irreversibility of a ferromagnet.
(b)The dissipated heat energy is directly proportional to the area of a hysteresis loop. A carbon steel piece has a greater hysteresis curve area. Hence, it dissipates greater heat energy.
(c)The value of magnetization is the memory or record of hysteresis loop cycles of magnetization. These bits of information correspond to the cycle of magnetization. Hysteresis loops can be used for storing information.
(d)Ceramic is used for coating magnetic tapes in cassette players and for building memory stores in modern computers.
(e)A certain region of space can be shielded from magnetic fields if it is surrounded by soft iron rings. In such arrangements, the magnetic lines are drawn out of the region.
Question 5.18:
A long straight horizontal cable carries a current of 2.5 A in the direction 10º south of west to 10° north of east. The magnetic meridian of the place happens to be 10º west of the geographic meridian. The earth’s magnetic field at the location is 0.33 G, and the angle of dip is zero. Locate the line of neutral points (ignore the thickness of the cable). (At neutral points, the magnetic field due to a current-carrying cable is equal and opposite to the horizontal component of the earth’s magnetic field.)
Solution:
Current in the wire, I = 2.5 A
The angle of dip at the given location on earth, δ = 0°
Earth’s magnetic field, H = 0.33 G = 0.33 × 10−4 T
The horizontal component of earth’s magnetic field is given as:
HH = H cos δ
= 0.33 x 10-4 x cos 0° = 0.33 x 10-4 T
The magnetic field at the neutral point at a distance R from the cable is given by the relation:
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
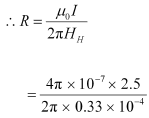
Hence, a set of neutral points parallel to and above the cable are located at a normal distance of 1.51 cm.
Question 5.19:
A telephone cable at a place has four long straight horizontal wires carrying a current of 1.0 A in the same direction east to west. The earth’s magnetic field at the place is 0.39 G, and the angle of dip is 35º. The magnetic declination is nearly zero. What are the resultant magnetic fields at points 4.0 cm below the cable?
Solution:
Number of horizontal wires in the telephone cable, n = 4
Current in each wire, I = 1.0 A
Earth’s magnetic field at a location, H = 0.39 G = 0.39 × 10−4 T
The angle of dip at the location, δ = 35°
The angle of declination, θ ∼ 0°
For a point 4 cm below the cable:
Distance, r = 4 cm = 0.04 m
The horizontal component of the earth’s magnetic field can be written as:
Hh = Hcosδ − B
Where,
B = Magnetic field at 4 cm due to current I in the four wires
= (4 x µ∘I) / (2πr)
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
= 0.2 × 10−4 T = 0.2 G
∴ Hh = 0.39 cos 35° − 0.2
= 0.39 × 0.819 − 0.2 ≈ 0.12 G
The vertical component of the magnetic field is given as:
Hv = Hsinδ
= 0.39 sin 35° = 0.22 G
The angle made by the field with its horizontal component is given as:
The resultant field at the point is given as:
For a point 4 cm above the cable:
Horizontal component of earth’s magnetic field:
Hh = Hcosδ + B
= 0.39 cos 35° + 0.2 = 0.52 G
Vertical component of earth’s magnetic field:
Hv = Hsinδ
= 0.39 sin 35° = 0.22 G
Angle, θ = 22.9°
And resultant field:
Question 5.20:
A compass needle free to turn in a horizontal plane is placed at the center of a circular coil of 30 turns and a radius of 12 cm. The coil is in a vertical plane making an angle of 45º with the magnetic meridian. When the current in the coil is 0.35 A, the needle points west to east.
(a) Determine the horizontal component of the earth’s magnetic field at the location.
(b) The current in the coil is reversed, and the coil is rotated about its vertical axis by an angle of 90º in the anticlockwise sense looking from above. Predict the direction of the needle. Take the magnetic declination at the places to be zero.
Solution:
Number of turns in the circular coil, N = 30
Radius of the circular coil, r = 12 cm = 0.12 m
Current in the coil, I = 0.35 A
The angle of dip, δ = 45°
(a) The magnetic field due to current I, at a distance r, is given as:
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
= 5.49 × 10−5 T
The compass needle points from West to East. Hence, the horizontal component of the earth’s magnetic field is given as:
BH = B sin δ
= 5.49 × 10−5 sin 45° = 3.88 × 10−5 T = 0.388 G
(b) When the current in the coil is reversed and the coil is rotated about its vertical axis by an angle of 90 º, the needle will reverse its original direction. In this case, the needle will point from East to West.
Question 5.21:
A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 60º, and one of the fields has a magnitude of 1.2 × 10−2 T. If the dipole comes to stable equilibrium at an angle of 15º with this field, what is the magnitude of the other field?
Solution:
The magnitude of one of the magnetic fields, B1 = 1.2 × 10−2 T
Magnitude of the other magnetic field = B2
The angle between the two fields, θ = 60°
At stable equilibrium, the angle between the dipole and field B1, θ1 = 15°
The angle between the dipole and field B2, θ2 = θ − θ1 = 60° − 15° = 45°
At rotational equilibrium, the torques between both the fields must balance each other.
∴The torque due to field B1 = Torque due to field B2
MB1 sinθ1 = MB2 sinθ2
Where,
M = Magnetic moment of the dipole
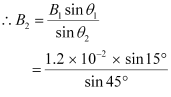
Hence, the magnitude of the other magnetic field is 4.39 × 10−3 T.
Question 5.22:
A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.04 G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (me= 9.11 × 10−19 C). [Note: Data in this exercise are so chosen that the answer will give you an idea of the effect of the earth’s magnetic field on the motion of the electron beam from the electron gun to the screen in a TV set.]
Solution:
Energy of an electron beam, E = 18 keV = 18 × 103 eV
Charge on an electron, e = 1.6 × 10−19 C
E = 18 × 103 × 1.6 × 10−19 J
Magnetic field, B = 0.04 G
Mass of an electron, me = 9.11 × 10−19 kg
Distance up to which the electron beam travels, d = 30 cm = 0.3 m
We can write the kinetic energy of the electron beam as:
E = mv²/2
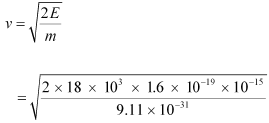
The electron beam deflects along a circular path of radius, r. The force due to the magnetic field balances the centripetal force of the path.
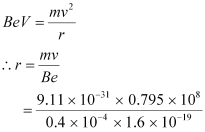
Let the up and down deflection of the electron beam be x = r(1-cosθ)
Where,
θ = Angle of declination
sinθ = d/r
= 0.3/11.3
θ = sin-1 (0.3/11.3) = 1.521°
And x = 11.3(1-cos1.521°)
= 0.0039 m = 3.9 mm
Therefore, the up and down deflection of the beam is 3.9 mm.
Question 5.23:
A sample of paramagnetic salt contains 2.0 × 1024 atomic dipoles each of dipole moment 1.5 × 10−23 J T−1. The sample is placed under a homogeneous magnetic field of 0.64 T and cooled to a temperature of 4.2 K. The degree of magnetic saturation achieved is equal to 15%. What is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K? (Assume Curie’s law)
Solution:
Number of atomic dipoles, n = 2.0 × 1024
Dipole moment of each atomic dipole, M = 1.5 × 10−23 J T−1
When the magnetic field, B1 = 0.64 T
The sample is cooled to a temperature, T1 = 4.2°K
Total dipole moment of the atomic dipole, Mtot = n × M
= 2 × 1024 × 1.5 × 10−23
= 30 J T−1
Magnetic saturation is achieved at 15%.
Hence, effective dipole moment,
When the magnetic field, B2 = 0.98 T
Temperature, T2 = 2.8°K
Its total dipole moment = M2
According to Curie’s law, we have the ratio of two magnetic dipoles as:
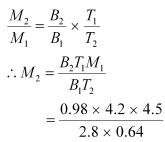
Therefore, 10.336 JT-1 is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K.
Question 5.24:
A Rowland ring of mean radius 15 cm has 3500 turns of wire wound on a ferromagnetic core of relative permeability 800. What is the magnetic field B in the core for a magnetizing current of 1.2 A?
Solution:
Mean radius of a Rowland ring, r = 15 cm = 0.15 m
Number of turns on a ferromagnetic core, N = 3500
Relative permeability of the core material, µr = 800
Magnetizing current, I = 1.2 A
The magnetic field is given by the relation:
B
Where,
µ∘ = Permeability of Free Space = 4π × 10–7 T m A–1
= 4.48 T
Therefore, the magnetic field in the core is 4.48 T.
Question 5.25:
The magnetic moment vectors μsand μlassociated with the intrinsic spin angular momentum S and orbital angular momentum l, respectively, of an electron, are predicted by quantum theory (and verified experimentally to a high accuracy) to be given by:
μs= –(e/m) S,
μl = –(e/2m)l
Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
Solution:
The magnetic moment associated with the orbital angular momentum is valid with classical mechanics.
The magnetic moment associated with the orbital angular momentum is given as
For current I and area of cross-section A, we have the relation:
Magnetic moment
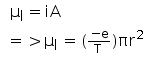
Where,
e= Charge of the electron
r= Radius of the circular orbit
T= Time taken to complete one rotation around the circular orbit of radius r
Orbital angular momentum, l= mvr
…….. (2)
Where,
m= Mass of the electron
v= Velocity of the electron
r= Radius of the circular orbit
Dividing equation (1) by equation (2), we get: