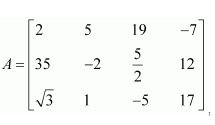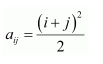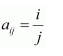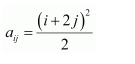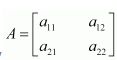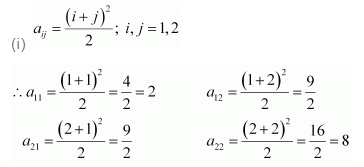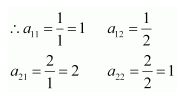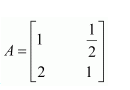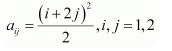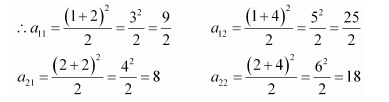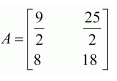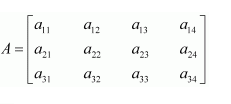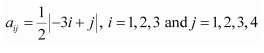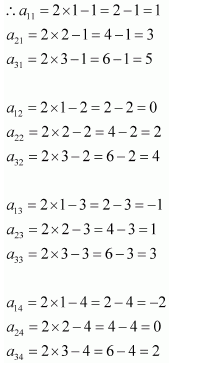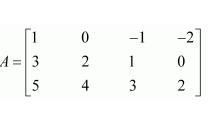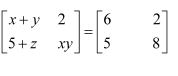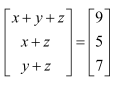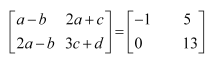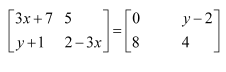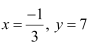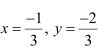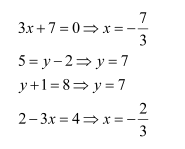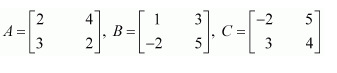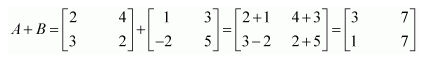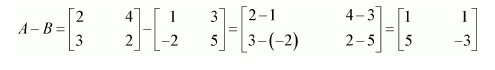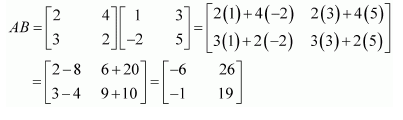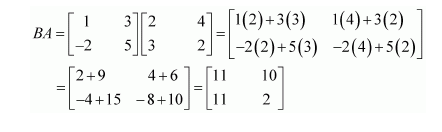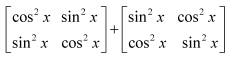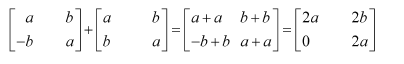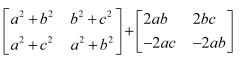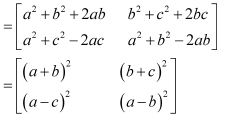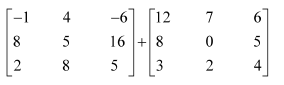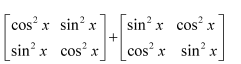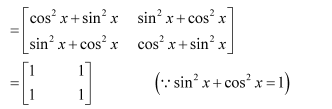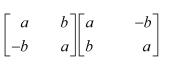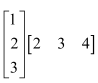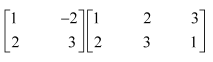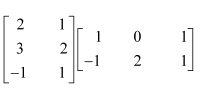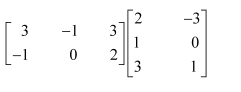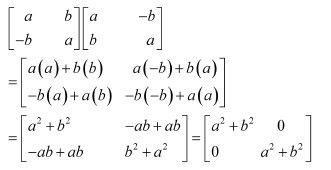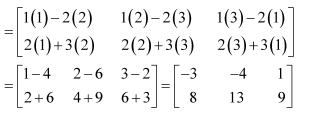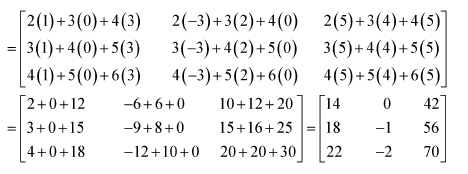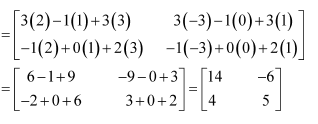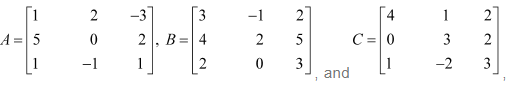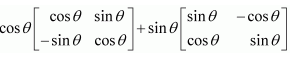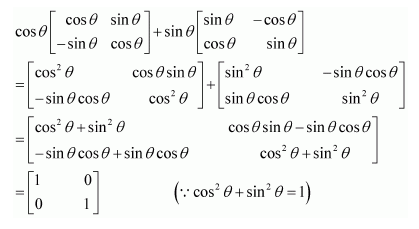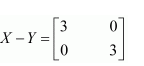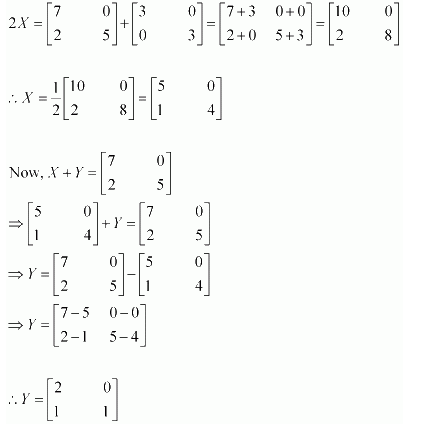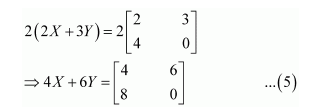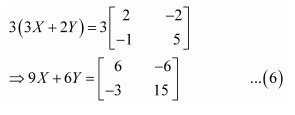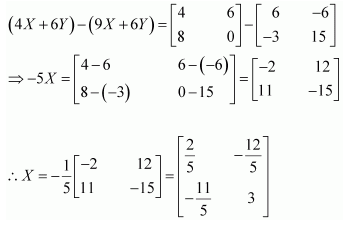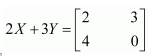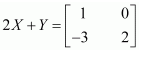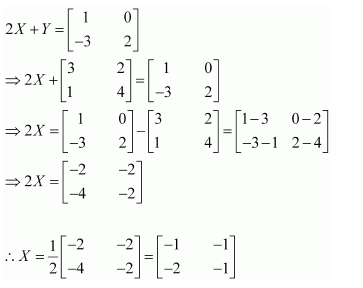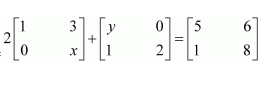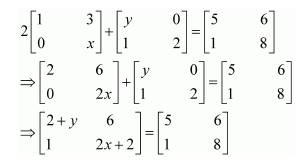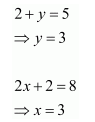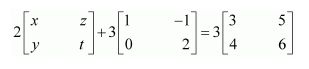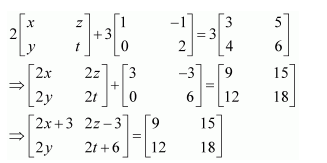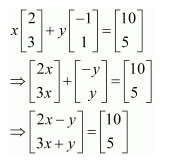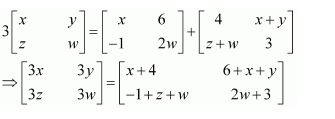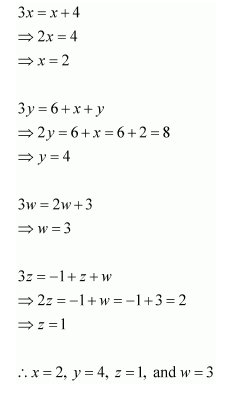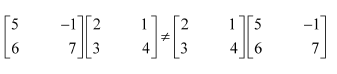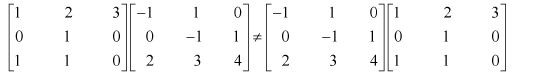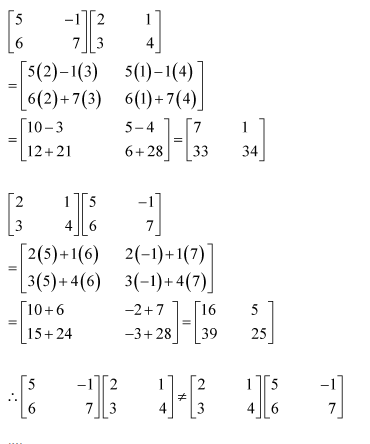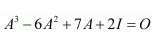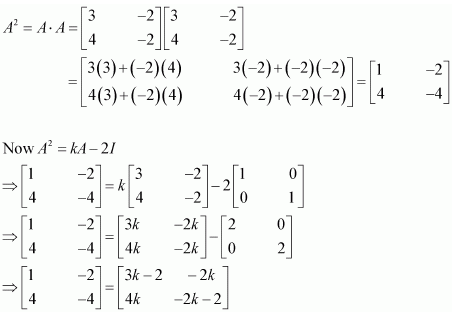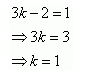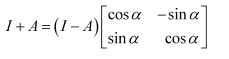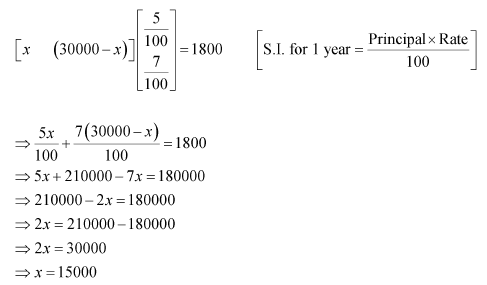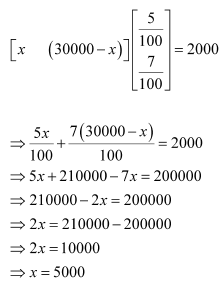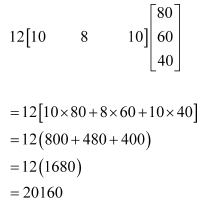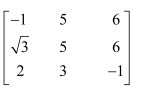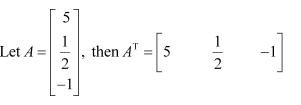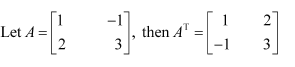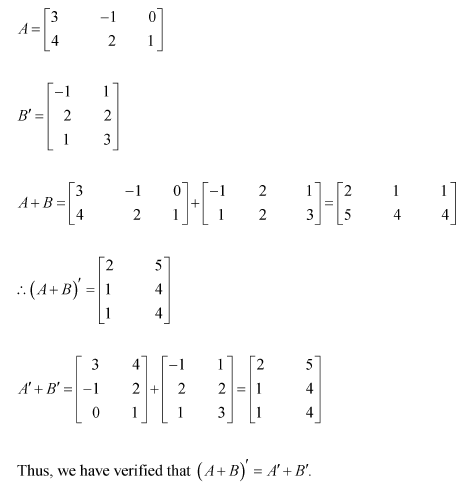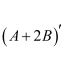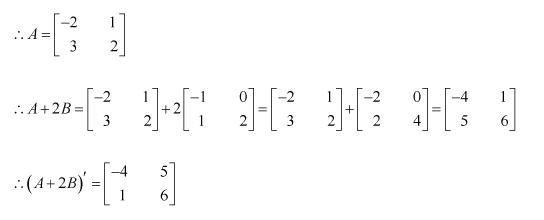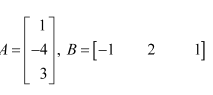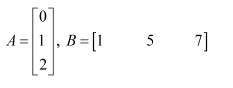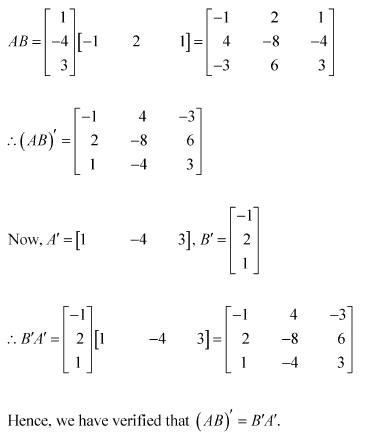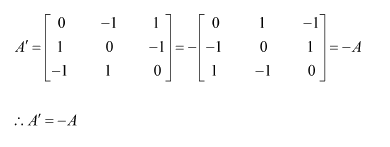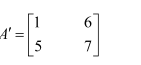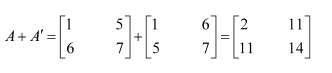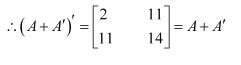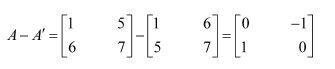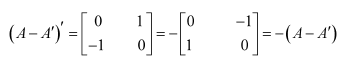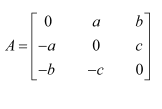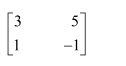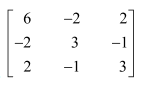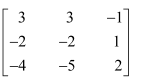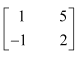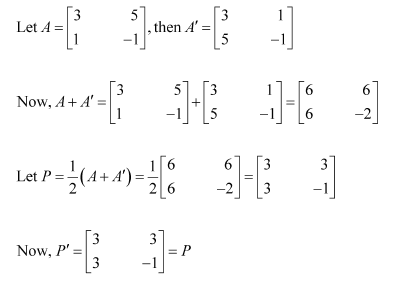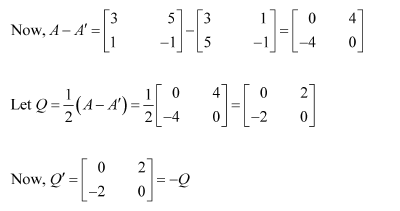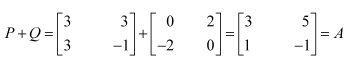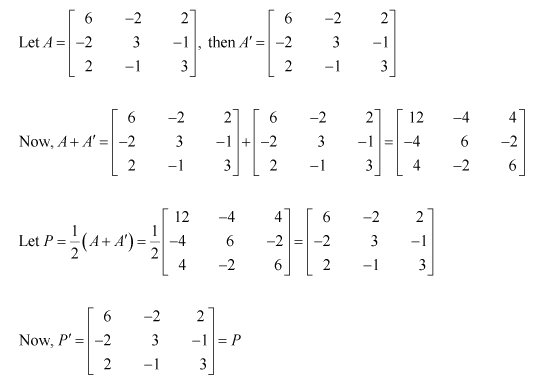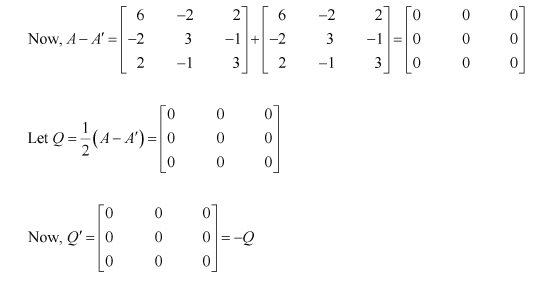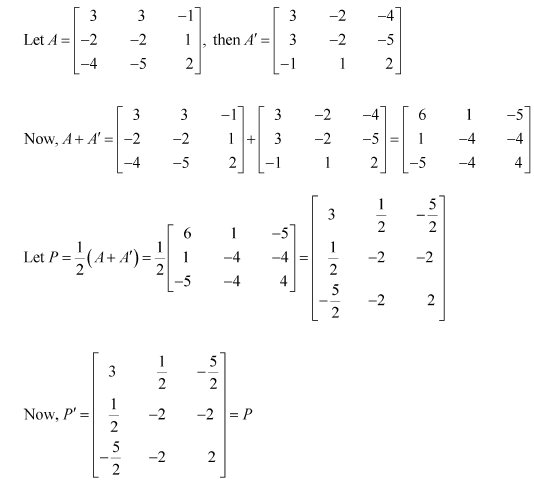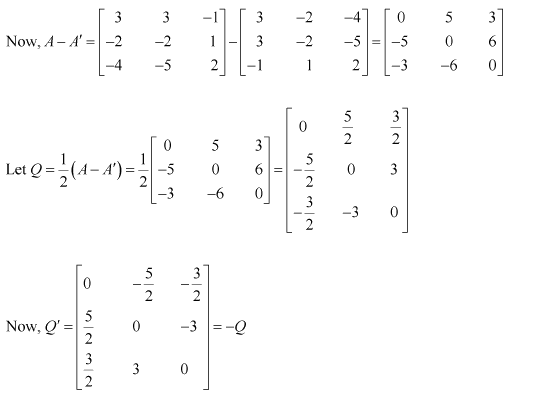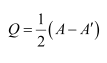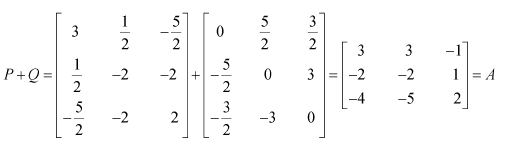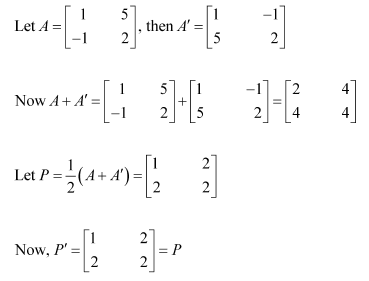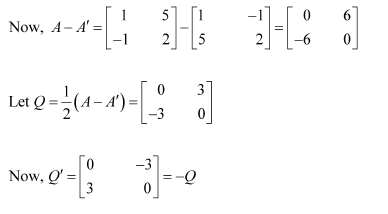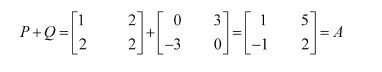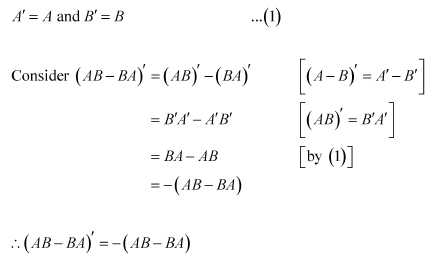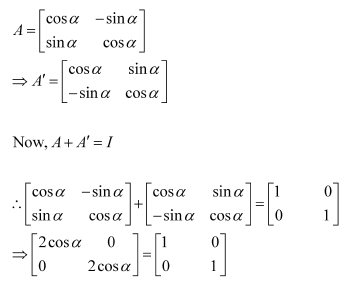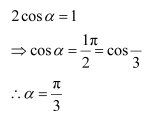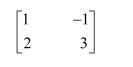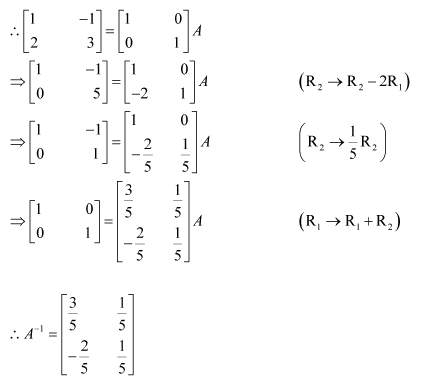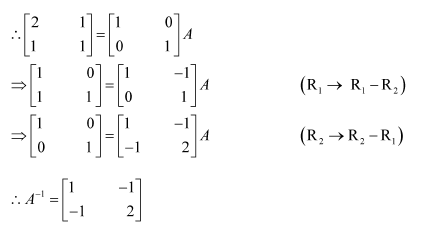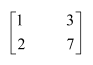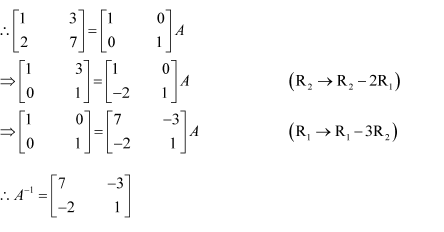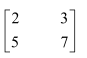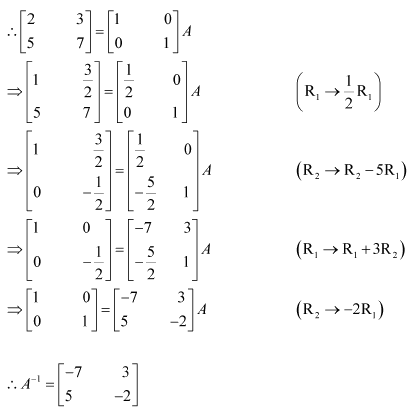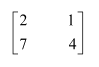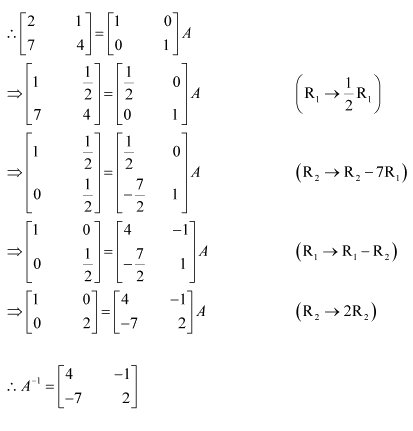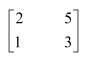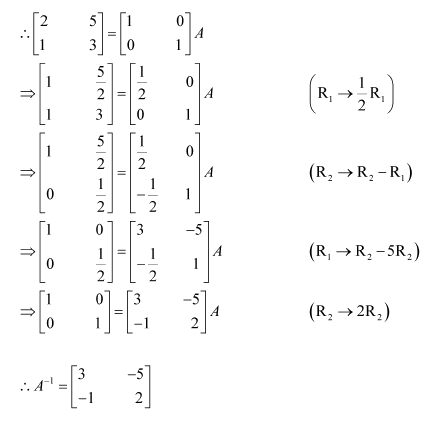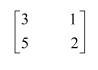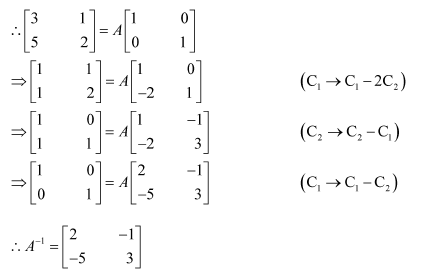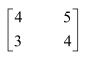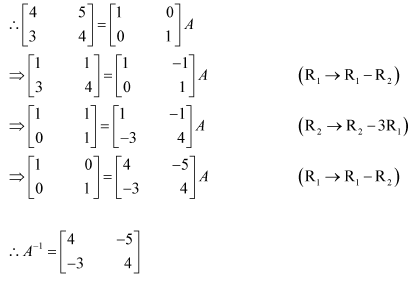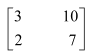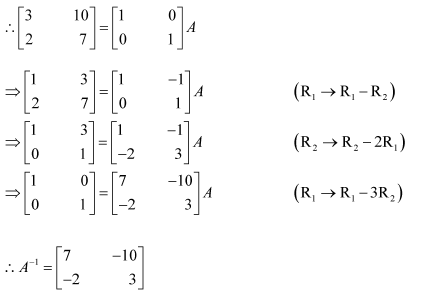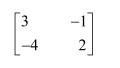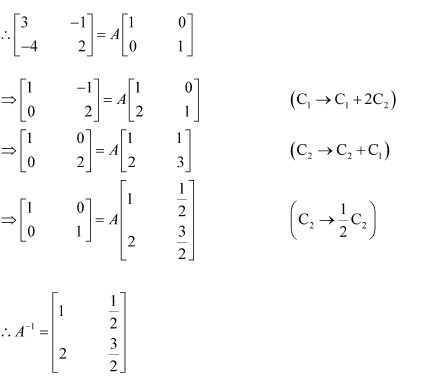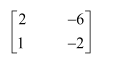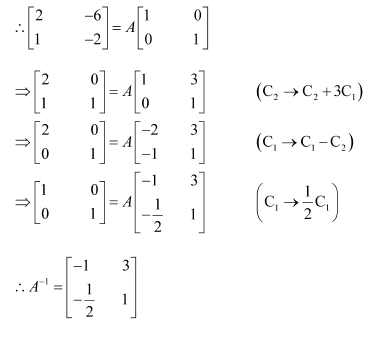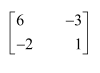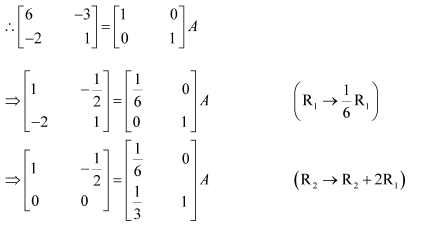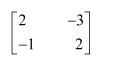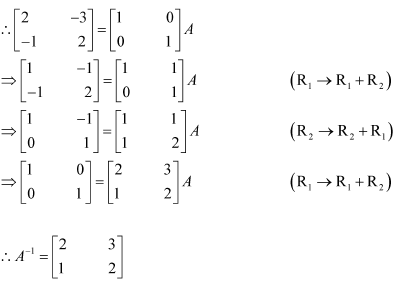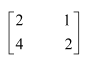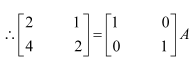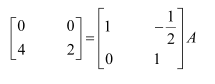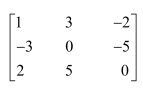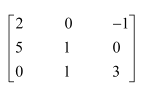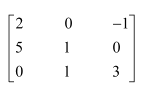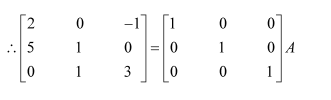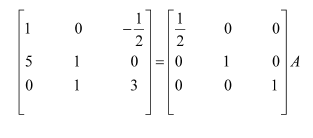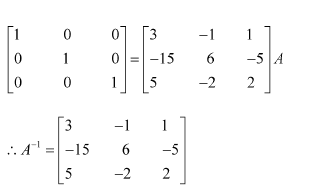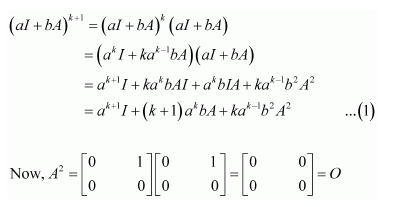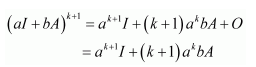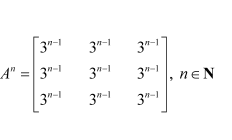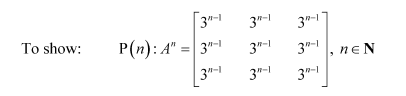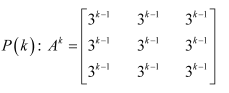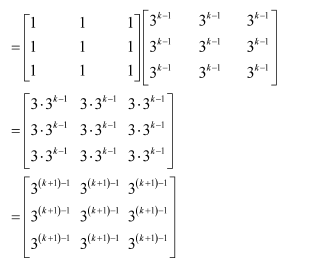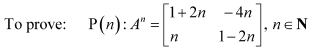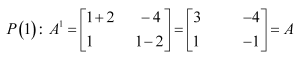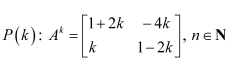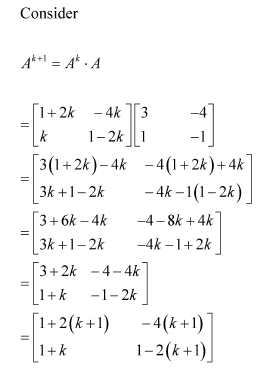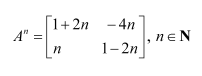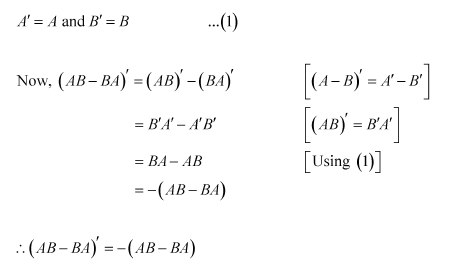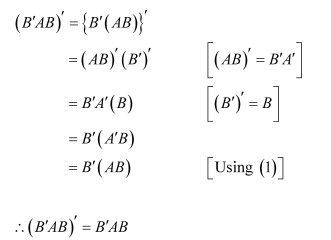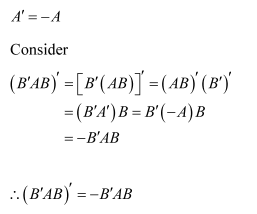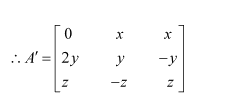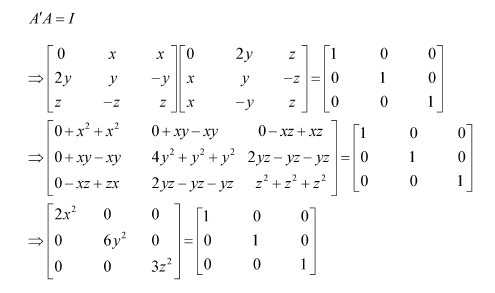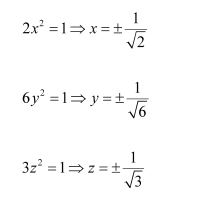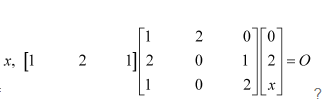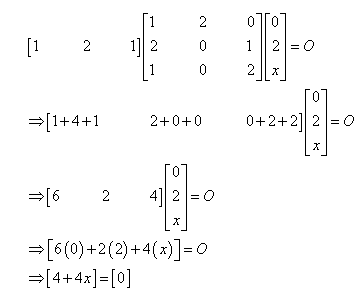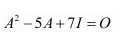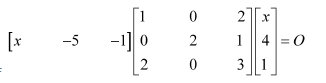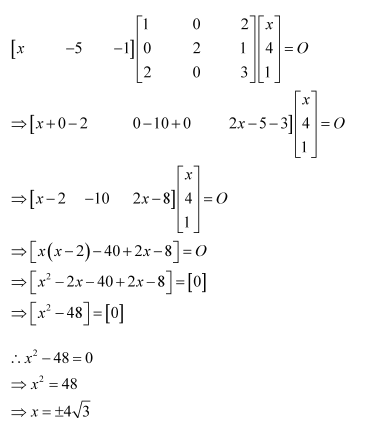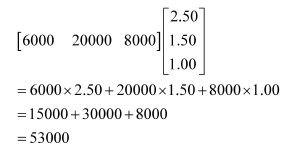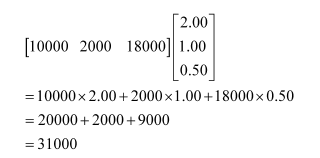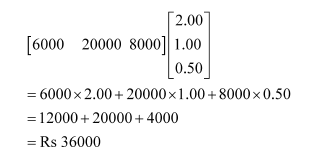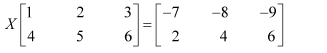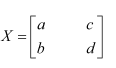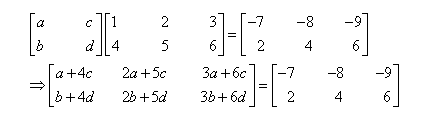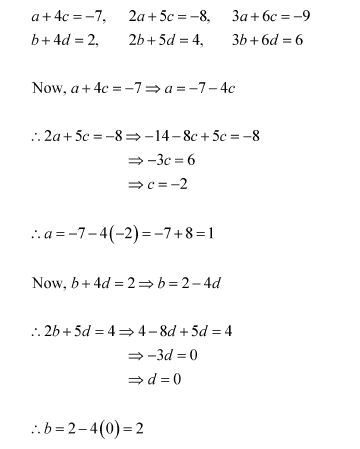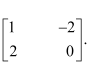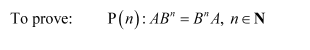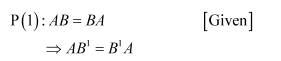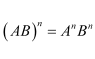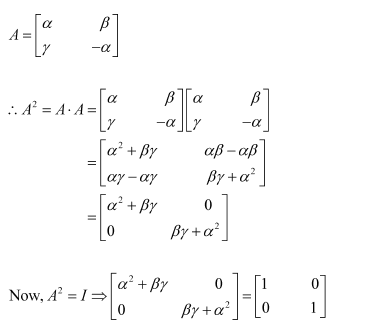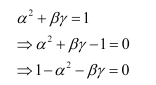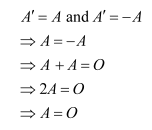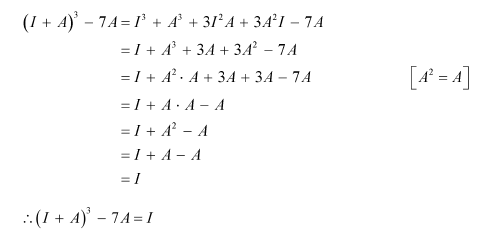NCERT Solutions For Class 12 Maths Chapter 3 covers all the exercises in the simplest method, which are solved by India’s best teachers. Students who are searching for Matrices Class 12 NCERT Solutions can easily approach this article. This can help you to solve the questions in an easy manner. Multiple times of practice of Matrices Class 12 notes give you the best result in the exam. The given table contains a list of subchapters of Class 12 Maths Matrices. Each solution was given in a detailed explanation. This can be helpful to get a better score in the examination. Class 12 NCERT Solutions Maths helps to complete your home assignments as well as revision purposes.
NCERT Solutions Of Class 12 Maths Chapter 3 Matrices
| Section Name | Topic Name |
| 3.1 | Introduction |
| 3.1 | Matrix |
| 3.3 | Types Of Matrices |
| 3.4 | Operations on Matrices |
NCERT Solutions For Class 12 Maths Chapter 3 Matrices Ex 3.1- Introduction
Question 1:
In the matrix
write:
(i) The order of the matrix (ii) The number of elements, (iii) Write the elements a13, a21, a33, a24, a23
Answer:
(i) In the given matrix, the number of rows is 3 and the number of columns is 4. Therefore, the order of the matrix is 3 × 4.
(ii) Since the order of the matrix is 3 × 4, there are 3 × 4 = 12 elements in it.
(iii) a13 = 19, a21 = 35, a33 = −5, a24 = 12, a23 =
Question 2:
If a matrix has 24 elements, what are the possible order it can have? What, if it has 13 elements?
Answer:
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numbers whose product is 24.
The ordered pairs are: (1, 24), (24, 1), (2, 12), (12, 2), (3, 8), (8, 3), (4, 6), and (6, 4)
Hence, the possible orders of a matrix having 24 elements are:
1 × 24, 24 × 1, 2 × 12, 12 × 2, 3 × 8, 8 × 3, 4 × 6, and 6 × 4
(1, 13) and (13, 1) are the ordered pairs of natural numbers whose product is 13.
Hence, the possible orders of a matrix having 13 elements are 1 × 13 and 13 × 1.
Question 3:
If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Answer:
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18.
The ordered pairs are: (1, 18), (18, 1), (2, 9), (9, 2), (3, 6,), and (6, 3)
Hence, the possible orders of a matrix having 18 elements are:
1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6, and 6 × 3
(1, 5) and (5, 1) are the ordered pairs of natural numbers whose product is 5.
Hence, the possible orders of a matrix having 5 elements are 1 × 5 and 5 × 1.
Question 4:
Construct a 2 × 2 matrix, 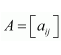
(i)
(ii)
(iii)
Answer:
In general, a 2 × 2 matrix is given by
Therefore, the required matrix is
(ii)
Therefore, the required matrix is
(iii)
Therefore, the required matrix is
Question 5:
Construct a 3 × 4 matrix, whose elements are given by
(i) 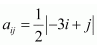
Answer:
In general, a 3 × 4 matrix is given by
(i)
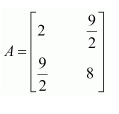
Therefore, the required matrix is
(ii)
Therefore, the required matrix is
Question 6:
Find the value of x, y, and z from the following equation:
(i) 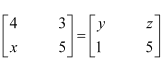
(iii)
Answer:
(i)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
x = 1, y = 4, and z = 3
(ii)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
x + y = 6, xy = 8, 5 + z = 5
Now, 5 + z = 5 ⇒ z = 0
We know that:
(x − y)2 = (x + y)2 − 4xy
⇒ (x − y)2 = 36 − 32 = 4
⇒ x − y = ±2
Now, when x − y = 2 and x + y = 6, we get x = 4 and y = 2
When x − y = − 2 and x + y = 6, we get x = 2 and y = 4
∴x = 4, y = 2, and z = 0 or x = 2, y = 4, and z = 0
(iii)
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
x + y + z = 9 … (1)
x + z = 5 … (2)
y + z = 7 … (3)
From (1) and (2), we have:
y + 5 = 9
⇒ y = 4
Then, from (3), we have:
4 + z = 7
⇒ z = 3
∴ x + z = 5
⇒ x = 2
∴ x = 2, y = 4, and z = 3
Question 7:
Find the value of a, b, c, and d from the equation:
Answer:
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
a − b = −1 … (1)
2a − b = 0 … (2)
2a + c = 5 … (3)
3c + d = 13 … (4)
From (2), we have:
b = 2a
Then, from (1), we have:
a − 2a = −1
⇒ a = 1
⇒ b = 2
Now, from (3), we have:
2 ×1 + c = 5
⇒ c = 3
From (4) we have:
3 ×3 + d = 13
⇒ 9 + d = 13 ⇒ d = 4
∴a = 1, b = 2, c = 3, and d = 4
Question 8:
is a square matrix, if
(A) m < n
(B) m > n
(C) m = n
(D) None of these
Answer:
The correct answer is C.
It is known that a given matrix is said to be a square matrix if the number of rows is equal to the number of columns.
Therefore, is a square matrix, if m = n.
Question 9:
Which of the given values of x and y make the following pair of matrices equal
(A)
(B) Not possible to find
(C)
(D)
Answer:
The correct answer is B.
It is given that
Equating the corresponding elements, we get:
We find that on comparing the corresponding elements of the two matrices, we get two different values of x, which is not possible.
Hence, it is not possible to find the values of x and y for which the given matrices are equal.
Question 10:
The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
(A) 27
(B) 18
(C) 81
(D) 512
Answer:
The correct answer is D.
The given matrix of the order 3 × 3 has 9 elements and each of these elements can be either 0 or 1.
Now, each of the 9 elements can be filled in two possible ways.
Therefore, by the multiplication principle, the required number of possible matrices is 29 = 512
Class 12 Maths Chapter 3 Matrices NCERT Solutions Ex 3.2 Matrix
Question 1:
Let
Find each of the following
(i) A+B (ii) A-B (iii) 3A-C (iv) AB (v) BA
Answer:
(i)
(ii)
(iii)
(iv) Matrix A has 2 columns. This number is equal to the number of rows in matrix B. Therefore, AB is defined as:
(v) Matrix B has 2 columns. This number is equal to the number of rows in matrix A. Therefore, BA is defined as:
Question 2:
Compute the following:
(i) 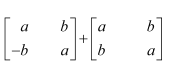
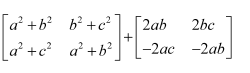
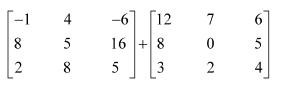
Answer:
(i)
(ii)
(iii)
(v)
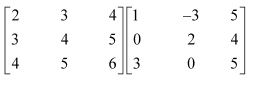
Question 3:
Compute the indicated products
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Answer:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Question 4:
If
then compute (A+B) and (B-C). Also verify that A+(B-C)=(A+B)-C.
Answer:
Hence we have verified that A+(B-C)=(A+B)-C
Question 5:
If 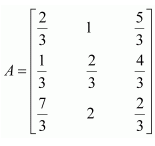
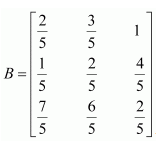
Answer:
Question 6:
Simplify
Answer:
Question 7:
Find X and Y, if
(i) 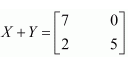
(ii) 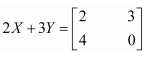
Answer:
(i) 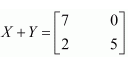
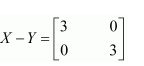
Adding equations (1) and (2), we get:
(ii)
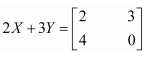
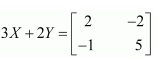
Multiplying equation (3) with (2), we get:
Multiplying equation (4) with (3), we get:
From (5) and (6), we have:
Now,
Question 8:
Find X, if 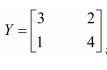
Answer:
Question 9:
Find x and y, if
Answer:
Comparing the corresponding elements of these two matrices, we have:
∴x = 3 and y = 3
Question 10:
Solve the equation for x, y, z, and t if
Answer:
Comparing the corresponding elements of these two matrices, we get:
Question 11:
If 
Answer:
Comparing the corresponding elements of these two matrices, we get:
2x − y = 10 and 3x + y = 5
Adding these two equations, we have:
5x = 15
⇒ x = 3
Now, 3x + y = 5
⇒ y = 5 − 3x
⇒ y = 5 − 9 = −4
∴x = 3 and y = −4
Question 12:
Given 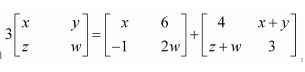
Answer:
Comparing the corresponding elements of these two matrices, we get:
Question 13:
If 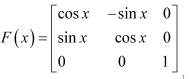
Answer:
Question 14:
Show that
(i)
(ii)
Answer:
(i)
(ii)
Question 15:
Find 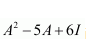
Answer:
We have A2 = A × A
Question 16:
If 
Answer:
Question 17:
If 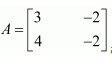
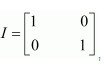
Answer:
Comparing the corresponding elements, we have:
Thus, the value of k is 1.
Question 18:
If 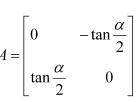
Answer:
Question 19:
A trust fund has Rs 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide Rs 30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) Rs 1,800 (b) Rs 2,000
Answer:
(a) Let Rs x be invested in the first bond. Then, the sum of money invested in the second bond will be Rs (30000 − x).
It is given that the first bond pays 5% interest per year and the second bond pays 7% interest per year.
Therefore, in order to obtain an annual total interest of Rs 1800, we have:
Thus, in order to obtain an annual total interest of Rs 1800, the trust fund should invest Rs 15000 in the first bond and the remaining Rs 15000 in the second bond.
(b) Let Rs x be invested in the first bond. Then, the sum of money invested in the second bond will be Rs (30000 − x).
Therefore, in order to obtain an annual total interest of Rs 2000, we have:
Thus, in order to obtain an annual total interest of Rs 2000, the trust fund should invest Rs 5000 in the first bond and the remaining Rs 25000 in the second bond.
Question 20:
The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, and 10 dozen economics books. Their selling prices are Rs 80, Rs 60 and Rs 40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.
Answer:
The bookshop has 10 dozen chemistry books, 8 dozen physics books, and 10 dozen economics books.
The selling prices of a chemistry book, a physics book, and an economics book are respectively given as Rs 80, Rs 60, and Rs 40.
The total amount of money that will be received from the sale of all these books can be represented in the form of a matrix as:
Thus, the bookshop will receive Rs 20160 from the sale of all these books.
Question 21:
Assume X, Y, Z, W, and P are matrices of order ,and
respectively. The restriction on n, k, and p that
will be defined are:
A. k = 3, p = n
B. k is arbitrary, p = 2
C. p is arbitrary, k = 3
D. k = 2, p = 3
Answer:
Matrices P and Y are of the orders p × k and 3 × k respectively.
Therefore, matrix PY will be defined if k = 3. Consequently, PY will be of the order p × k.
Matrices W and Y are of the orders n × 3 and 3 × k respectively.
Since the number of columns in W is equal to the number of rows in Y, matrix WY is well-defined and is of the order n × k.
Matrices PY and WY can be added only when their orders are the same.
However, PY is of the order p × k and WY is of the order n × k. Therefore, we must have p = n.
Thus, k = 3 and p = n are the restrictions on n, k, and p so that PY+WY will be defined.
Question 22:
Assume X, Y, Z, W, and P are matrices of order 2×n, 3×k, 2×p, n×3, and p× k respectively. If n = p, then the order of the matrix 7x-5z is A p × 2 B 2 × n C n× 3 D p× n
Answer:
The correct answer is B.
Matrix X is of the order 2 × n.
Therefore, matrix 7X is also of the same order.
Matrix Z is of the order 2 × p, i.e., 2 × n [Since n = p]
Therefore, matrix 5Z is also of the same order.
Now, both the matrices 7X and 5Z are of the order 2 × n.
Thus, matrix 7X − 5Z is well-defined and is of the order 2 × n.
NCERT Solutions For Class 12 Maths Chapter 3 Matrices Ex 3.3 Types of Matrices
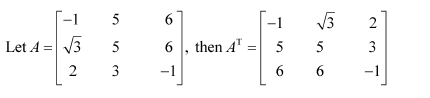
Question 1:
Find the transpose of each of the following matrices:
(i) (ii)
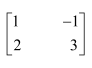
Answer:
(i)
(ii)
(iii)
Question 2:
If 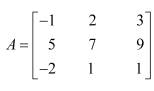
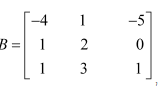
(i)
(ii)
Answer:
We have
(i)
(ii)
Question 3:
If 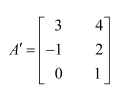

(i)
(ii)
Answer:
(i) It is known that
Therefore, we have:
(ii)
Question 4:
If 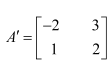
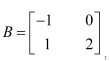
Answer:
We know that
Question 5:
For the matrices A and B, verify that (AB)′ = where
(i)
(ii)
Answer:
(i)
(ii)
Question 6:
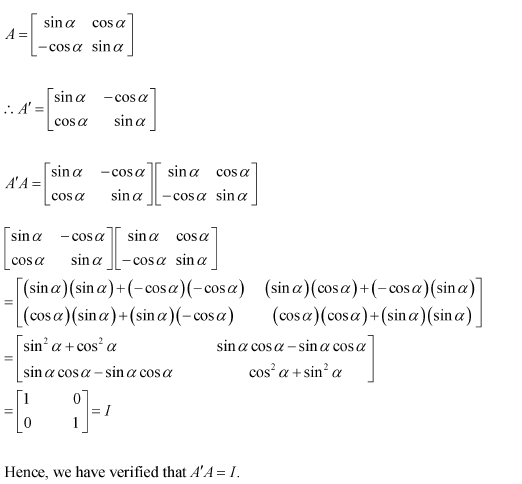
If (i) 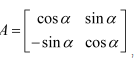
(ii) 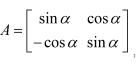
Answer:
(i)
(ii)
Question 7:
(i) Show that the matrix 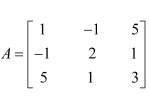
(ii) Show that the matrix 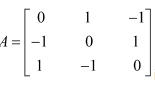
Answer:
(i) We have:
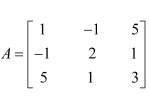
Hence, A is a symmetric matrix.
(ii) We have:
Hence, A is a skew-symmetric matrix.
Question 8:
For the matrix 
(i) is a symmetric matrix
(ii) is a skew-symmetric matrix
Answer:
(i)
Hence,
is a symmetric matrix.
(ii)
Hence,
is a skew-symmetric matrix.
Question 9:
Find
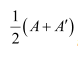
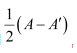
Answer:
The given matrix is
Question 10:
Express the following matrices as the sum of a symmetric and a skew symmetric matrix:
(i)
(ii)
(iii)
(iv)
Answer:
(i)
Thus 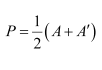
thus 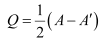
Representing A as the sum of P and Q:
(ii)
thus 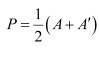
thus
is a skew-symmetric matrix.
Representing A as the sum of P and Q:
(iii)
thus 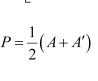
thus
is a skew-symmetric matrix.
Representing A as the sum of P and Q:
(iv)
thus 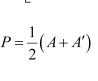
thus
is a skew-symmetric matrix.
Representing A as the sum of P and Q:
Question 11:
If A, B are symmetric matrices of the same order, then AB − BA is a
A. Skew symmetric matrix B. Symmetric matrix
C. Zero matrix D. Identity matrix
Answer:
The correct answer is A.
A and B are symmetric matrices, therefore, we have:
Thus, (AB − BA) is a skew-symmetric matrix
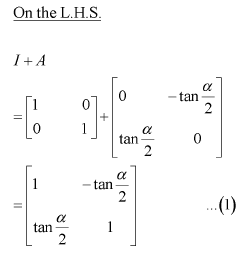
Question 12:
If 
if the value of α is
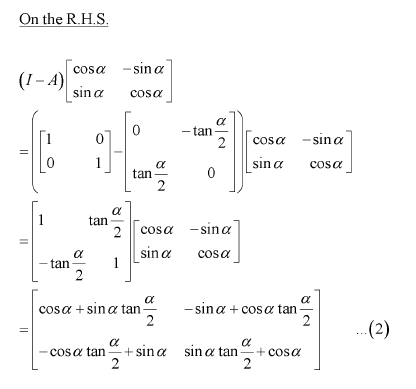
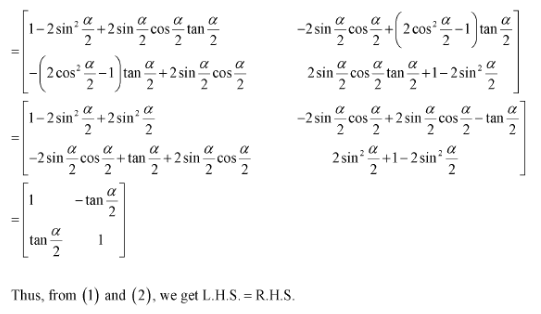
(A) (B)
(C) π (D)
Answer:
The correct answer is B.
Comparing the corresponding elements of the two matrices, we have:
NCERT Solutions For Class 12 Maths Chapter 3 Matrices Ex 3.4 Operations On Matrices
Question 1:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 2:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 3:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 4:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 5:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 6:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 7:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = AI
Question 8:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 9:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 10:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = AI
Question 11:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = AI
Question 12:
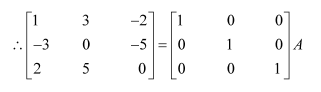
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Now, in the above equation, we can see all the zeros in the second row of the matrix on the L.H.S.
Therefore, A−1 does not exist.
Question 13:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 14:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
applying 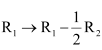
Now, in the above equation, we can see all the zeros in the first row of the matrix on the L.H.S.
Therefore, A−1 does not exist.
Question 15:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Question 16:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Applying R2 → R2 + 3R1 and R3 → R3 − 2R1, we have:
Question 17:
Find the inverse of each of the matrices, if it exists.
Answer:
Let A=
We know that A = IA
Applying 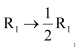
Question 18:
Matrices A and B will be inverse of each other only if
A. AB = BA
C. AB = 0, BA = I
B. AB = BA = 0
D. AB = BA = I
Answer:
Answer: D
We know that if A is a square matrix of order m, and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is said to be the inverse of A. In this case, it is clear that A is the inverse of B.
Thus, matrices A and B will be inverses of each other only if AB = BA = I.
NCERT Solutions For Class 12 Maths Chapter 3 Matrices Miscellaneous Solutions
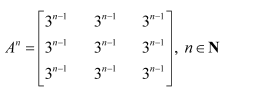
Question 1:
Let 
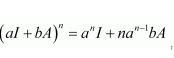
Answer:
It is given that
We shall prove the result by using the principle of mathematical induction.
For n = 1, we have:
Therefore, the result is true for n = 1.
Let the result be true for n = k.
That is,
Now, we prove that the result is true for n = k + 1.
Consider
From (1), we have:
Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have:
Question 2:
If 
Answer:
It is given that
We shall prove the result by using the principle of mathematical induction.
For n = 1, we have:
Therefore, the result is true for n = 1.
Let the result be true for n = k.
That is
Now, we prove that the result is true for n = k + 1.
Therefore, the result is true for n = k + 1.
Thus by the principle of mathematical induction, we have:
Question 3:
If 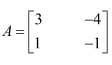
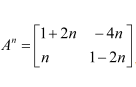
Answer:
It is given that
We shall prove the result by using the principle of mathematical induction.
For n = 1, we have:
Therefore, the result is true for n = 1.
Let the result be true for n = k.
That is,
Now, we prove that the result is true for n = k + 1.
Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have:
Question 4:
If A and B are symmetric matrices, prove that AB − BA is a skew symmetric matrix
Answer:
It is given that A and B are symmetric matrices. Therefore, we have:
Thus, (AB − BA) is a skew-symmetric matrix.
Question 5:
Show that the matrix is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Answer:
We suppose that A is a symmetric matrix, then ….(1) consider
Thus, if A is a symmetric matrix, then
is a symmetric matrix.
Now, we suppose that A is a skew-symmetric matrix.
Then,
Thus, if A is a skew-symmetric matrix, then
is a skew-symmetric matrix.
Hence, if A is a symmetric or skew-symmetric matrix, then is a symmetric or skew-symmetric matrix accordingly.
Question 6:
Find the values of x, y, z if the matrix 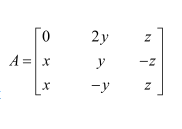
Answer:
It is given that
Now,
On comparing the corresponding elements, we have:
Question 7:
For what values of
Answer:
We have
∴4 + 4x = 0
⇒ x = −1
Thus, the required value of x is −1.
Question 8:
If 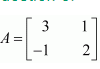
Answer:
Question 9:
Find x, if
Answer:
We have:
Question 10:
A manufacturer produces three products x, y, z which he sells in two markets.
Annual sales are indicated below:
|
Market |
Products |
||
|
I |
10000 |
2000 |
18000 |
|
II |
6000 |
20000 |
8000 |
(a) If unit sale prices of x, y and z are Rs 2.50, Rs 1.50 and Rs 1.00, respectively, find the total revenue in each market with the help of matrix algebra.
(b) If the unit costs of the above three commodities are Rs 2.00, Rs 1.00 and 50 paise respectively. Find the gross profit.
Answer:
(a) The unit sale prices of x, y, and z are respectively given as Rs 2.50, Rs 1.50, and Rs 1.00.
Consequently, the total revenue in market I can be represented in the form of a matrix as:
The total revenue in market II can be represented in the form of a matrix as:
Therefore, the total revenue in market I isRs 46000 and the same in market II isRs 53000.
(b) The unit cost prices of x, y, and z are respectively given as Rs 2.00, Rs 1.00, and 50 paise.
Consequently, the total cost prices of all the products in market I can be represented in the form of a matrix as:
Since the total revenue in market I isRs 46000, the gross profit in this marketis (Rs 46000 − Rs 31000) Rs 15000.
The total cost prices of all the products in market II can be represented in the form of a matrix as:
Since the total revenue in market II isRs: 53000, the gross profit in this market is (Rs:53000 − Rs: 36000) Rs:17000.
Question 11:
Find the matrix X so that
Answer:
It is given that:
The matrix given on the R.H.S. of the equation is a 2 × 3 matrix and the one given on the L.H.S. of the equation is a 2 × 3 matrix. Therefore, X has to be a 2 × 2 matrix.
Now, let
Therefore, we have:
Equating the corresponding elements of the two matrices, we have:
Thus, a = 1, b = 2, c = −2, d = 0
Hence, the required matrix X is
Question 12:
If A and B are square matrices of the same order such that AB =BA, then prove by induction that Further, prove that
for all n ∈ N
Answer:
A and B are square matrices of the same order such that AB = BA.
For n = 1, we have:
Therefore, the result is true for n = 1.
Let the result be true for n = k.
Now, we prove that the result is true for n = k + 1.
Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
Now, we prove that
for all n ∈ N
For n = 1, we have:
Now, we prove that the result is true for n = k + 1.
Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
for all natural numbers.
Question 13:
Choose the correct answer in the following questions:
If 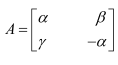
then
(A)
(B)
(C)
(D)
Answer:
Answer: C
On comparing the corresponding elements, we have:
Question 14:
If the matrix A is both symmetric and skew symmetric, then
A. A is a diagonal matrix
B. A is a zero matrix
C. A is a square matrix
D. None of these
Answer:
Answer: B
If A is both symmetric and skew-symmetric matrix, then we should have
Therefore, A is a zero matrix.
Question 15:
If A is a square matrix such that 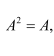
is equal to
A. A B. I − A C. I D. 3A
Answer:
Answer: C