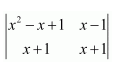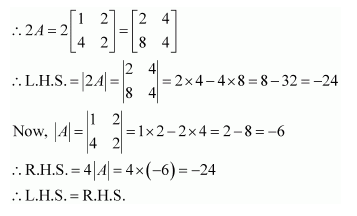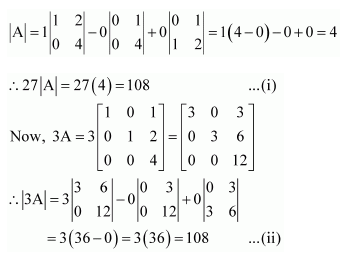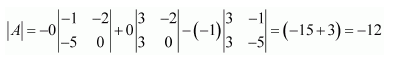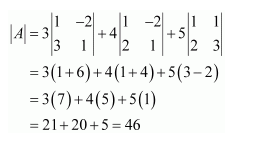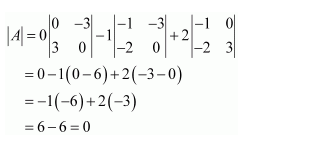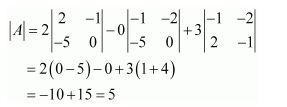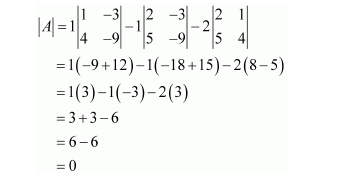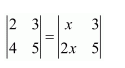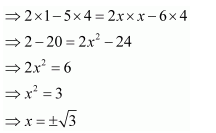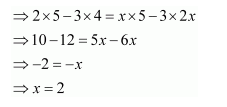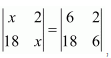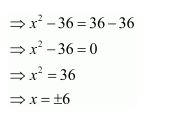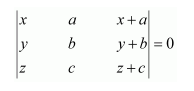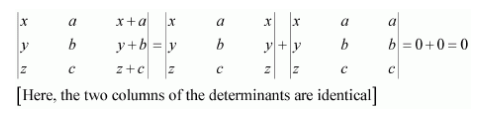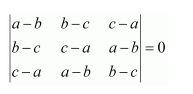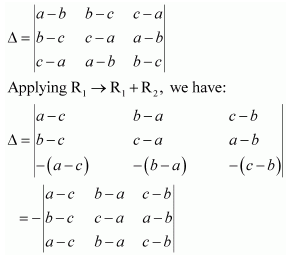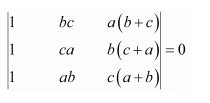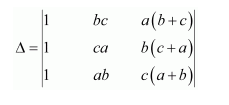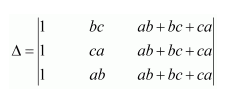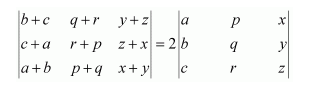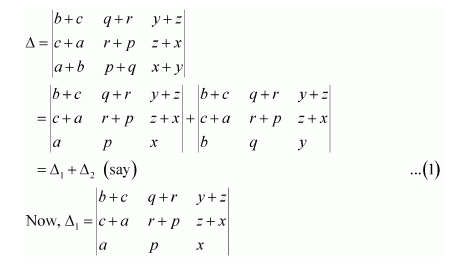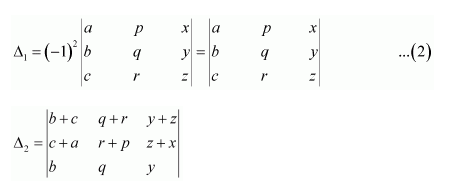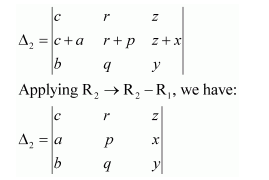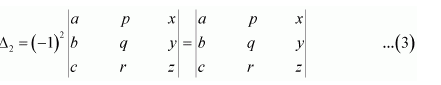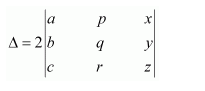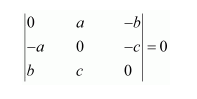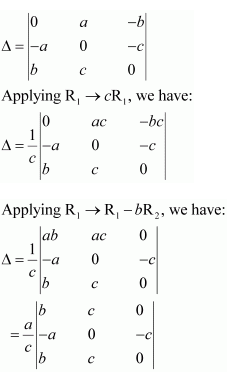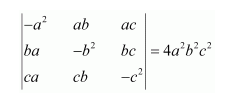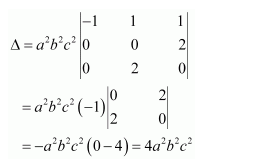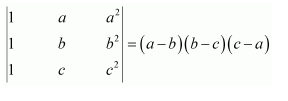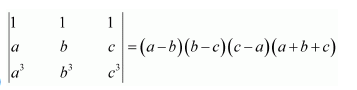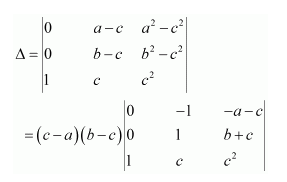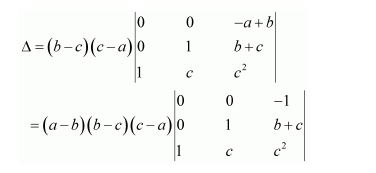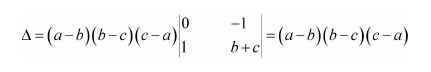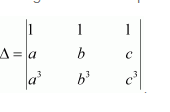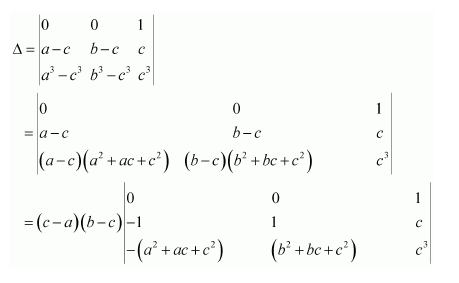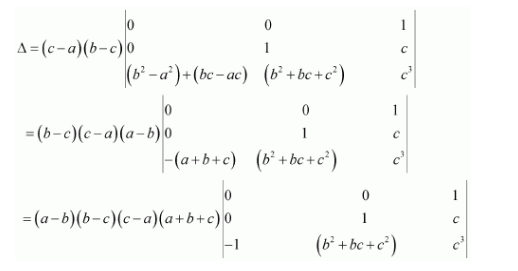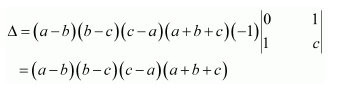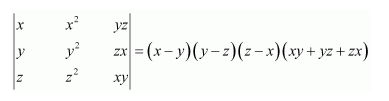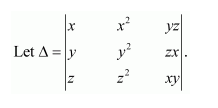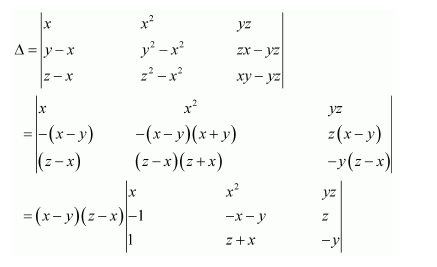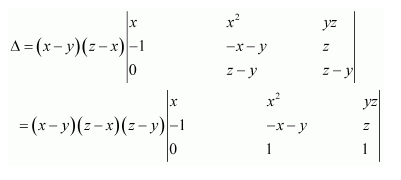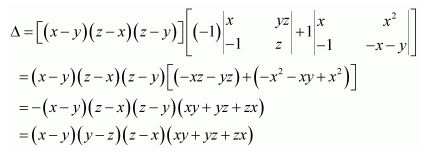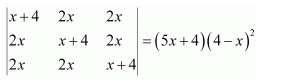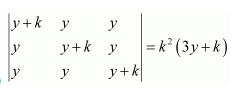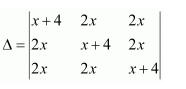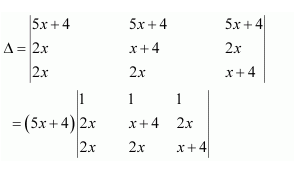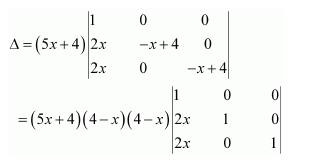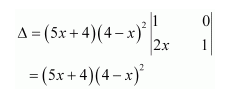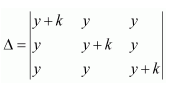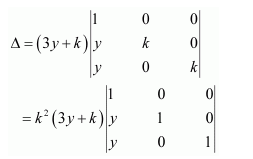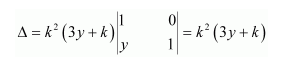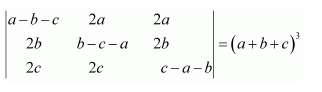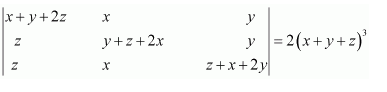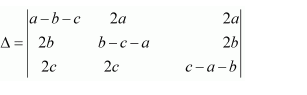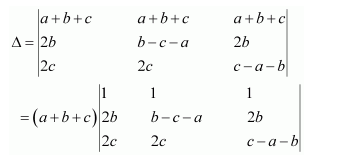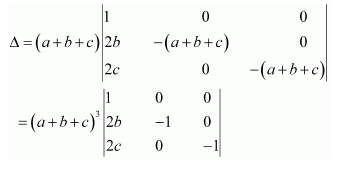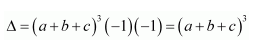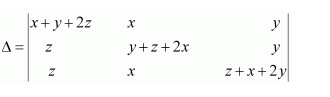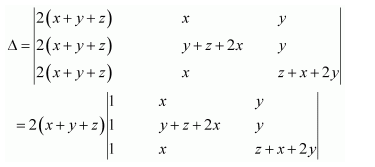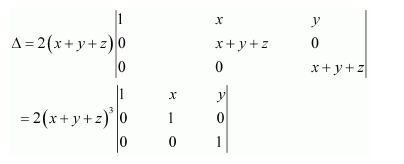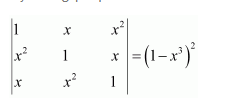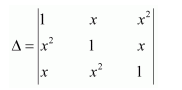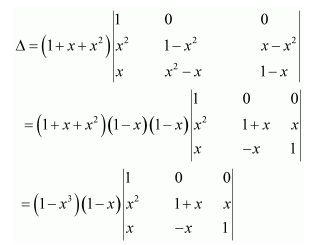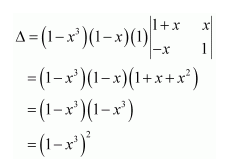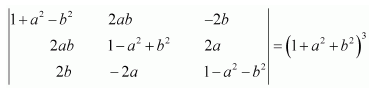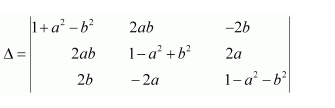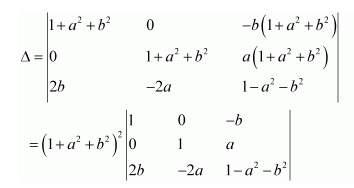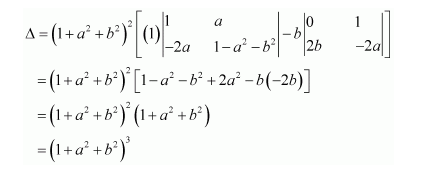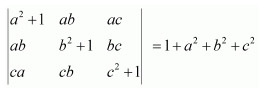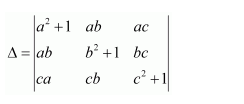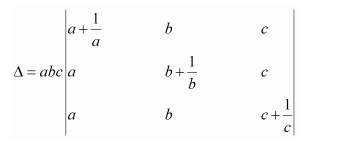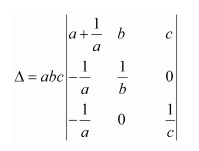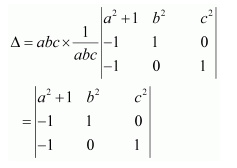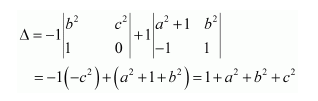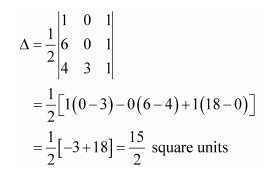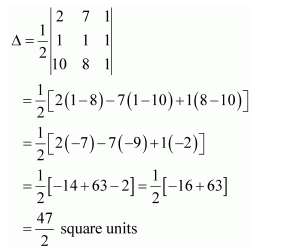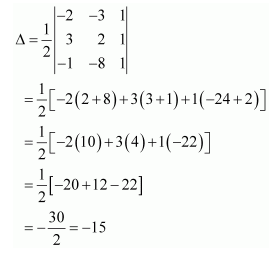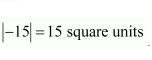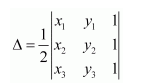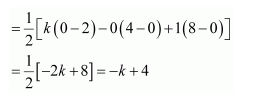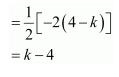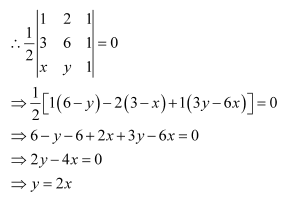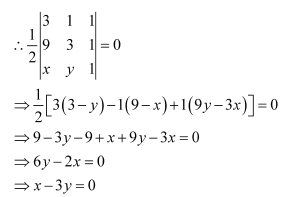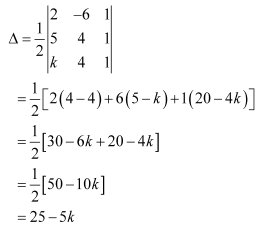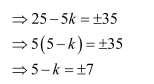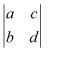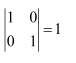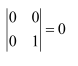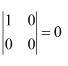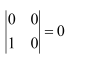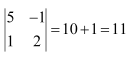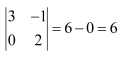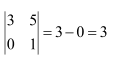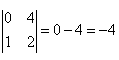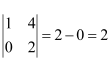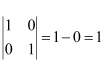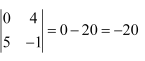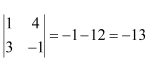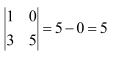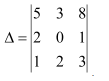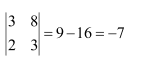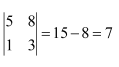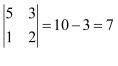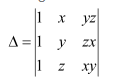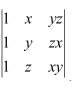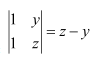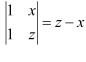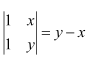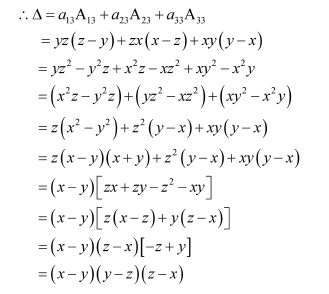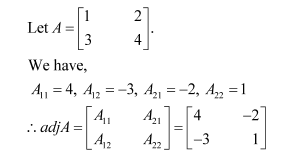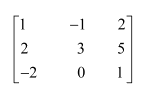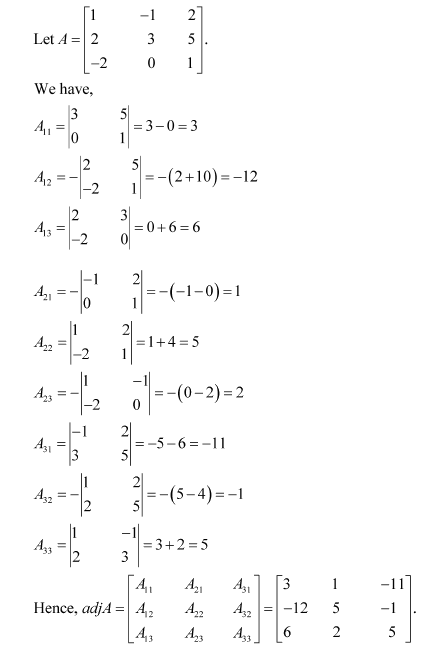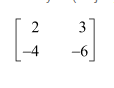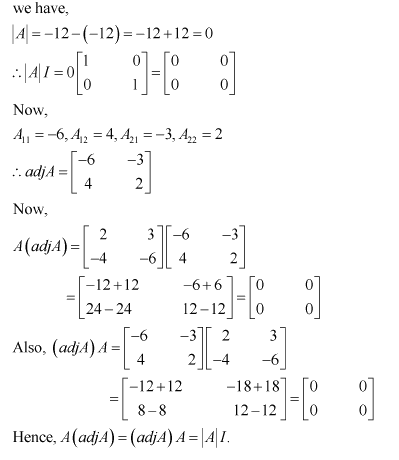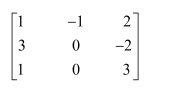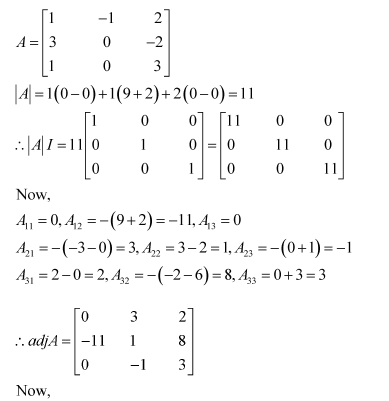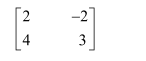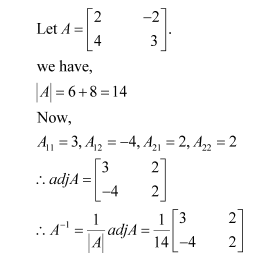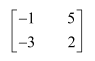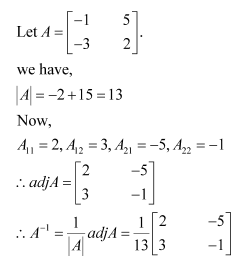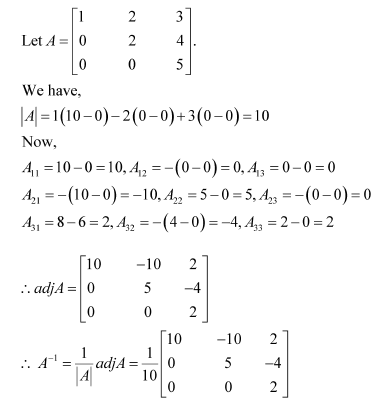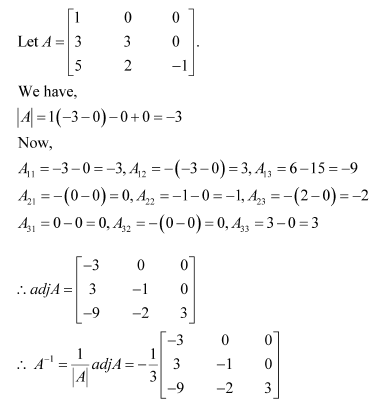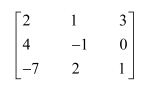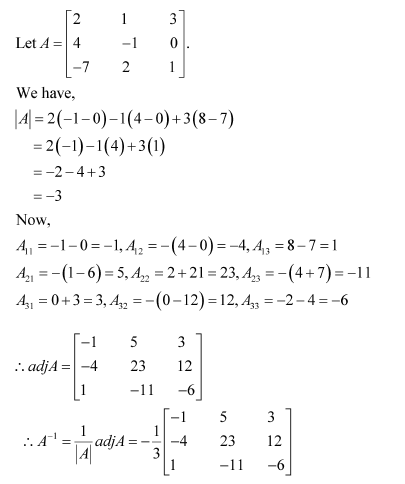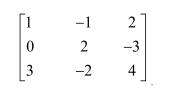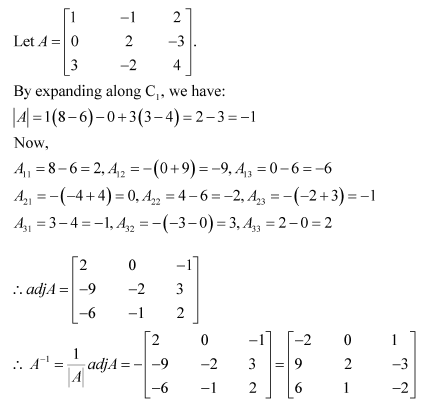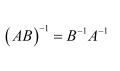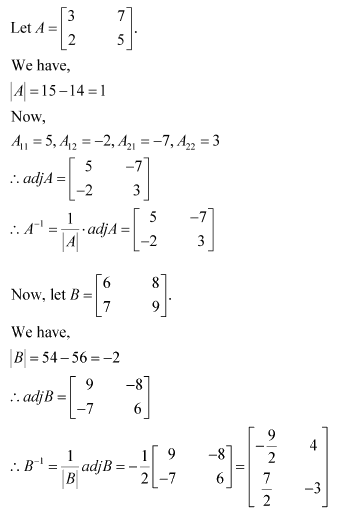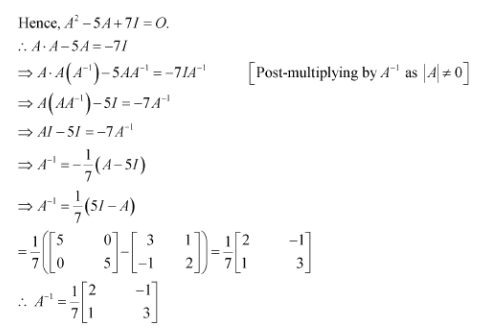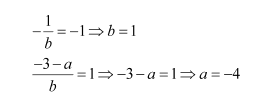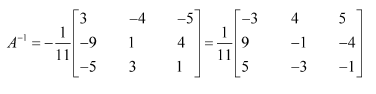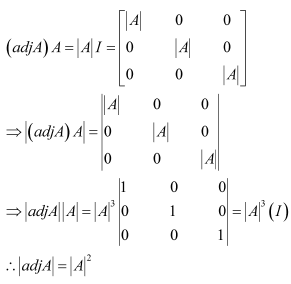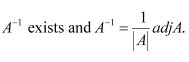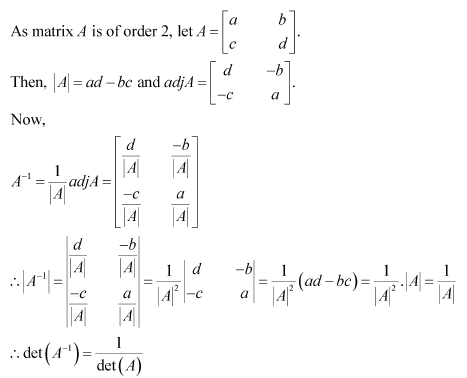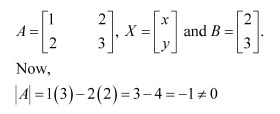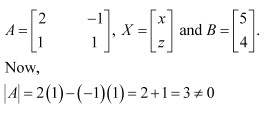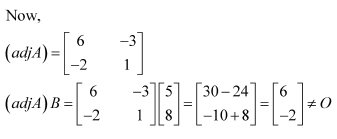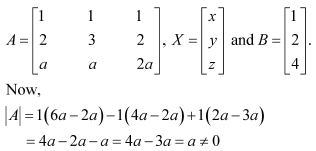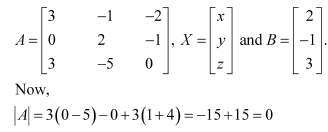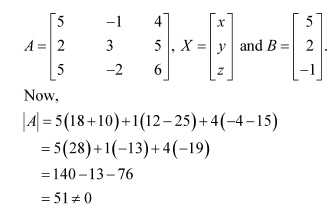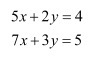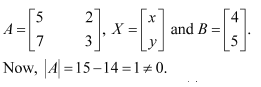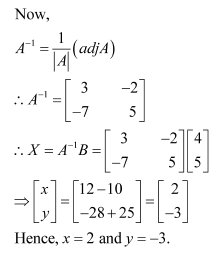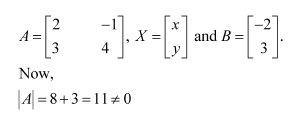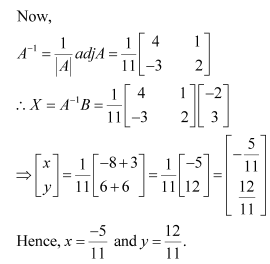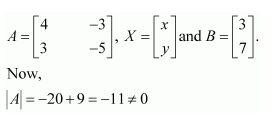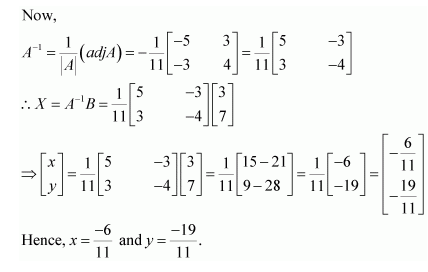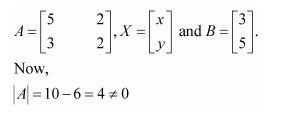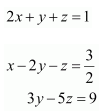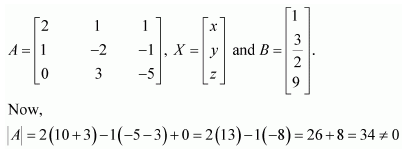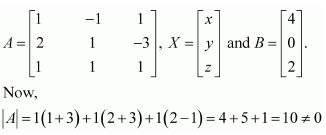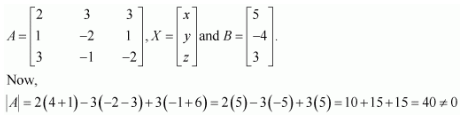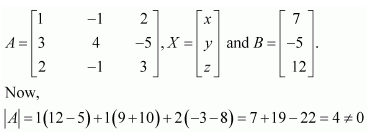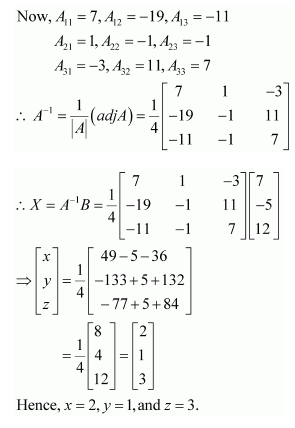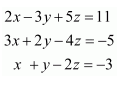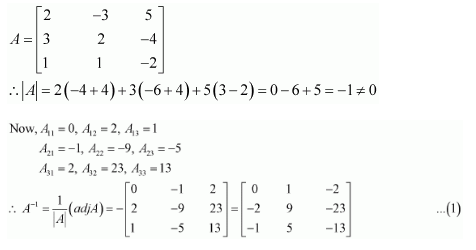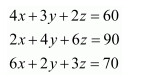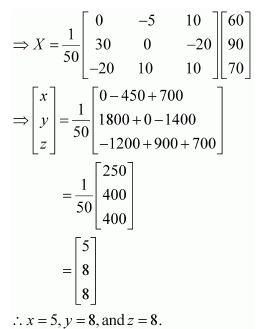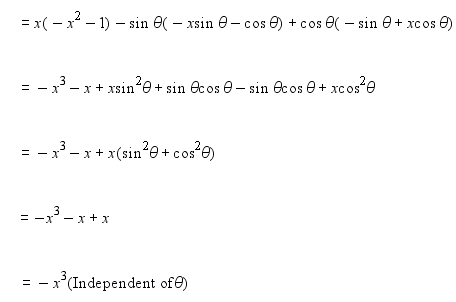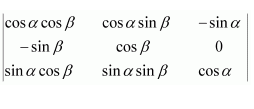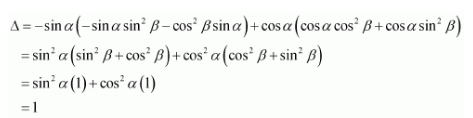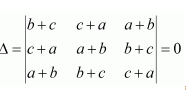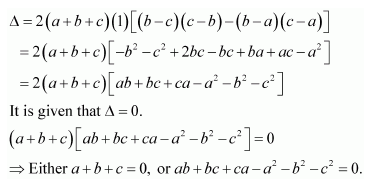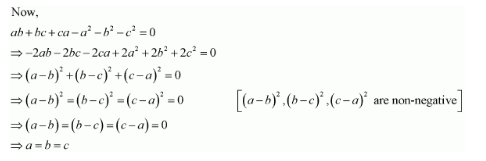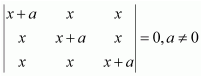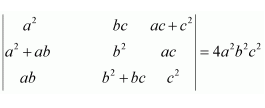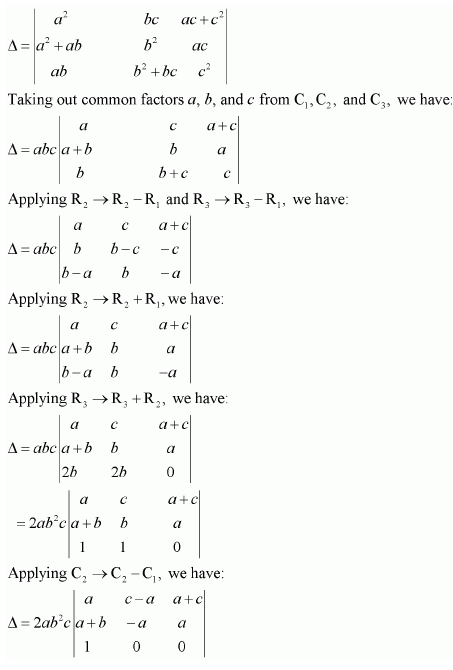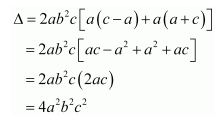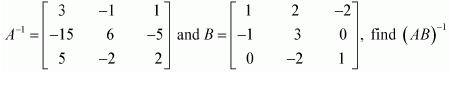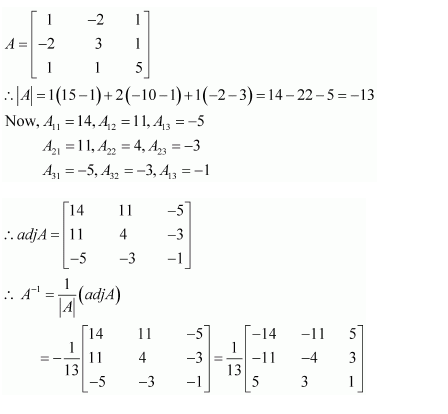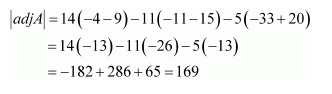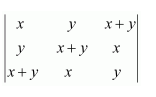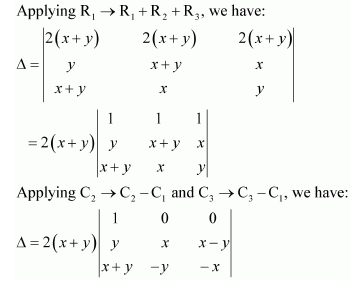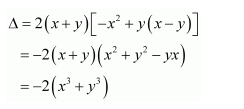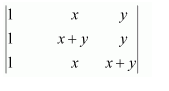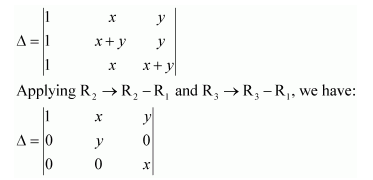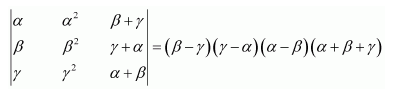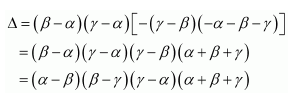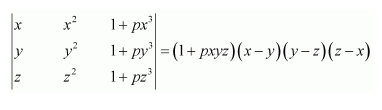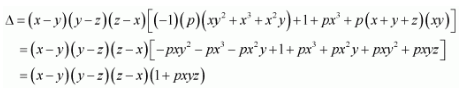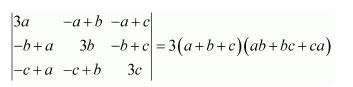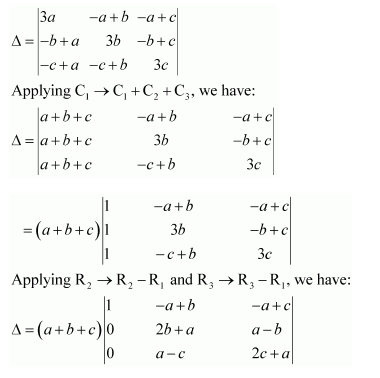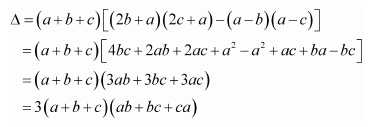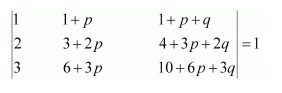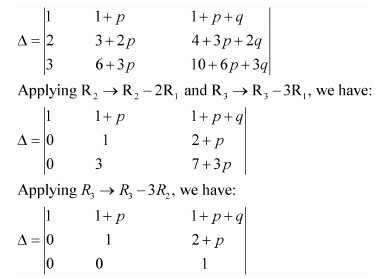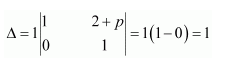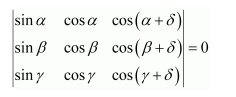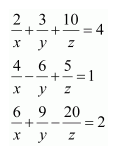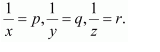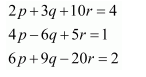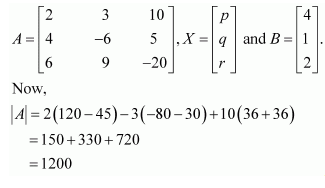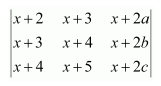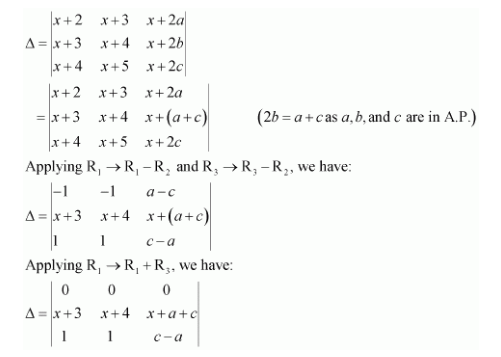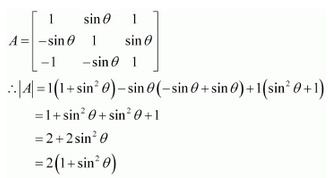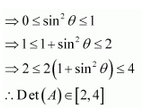NCERT Solutions For Class 12 Maths Chapter 4

NCERT Solutions For Class 12 Maths Chapter 4 will clear all the doubts which were related to the 4th chapter. Class 12 Maths NCERT Solutions will help in improving your problem-solving abilities. Students must practice the Class 12 Maths NCERT Book Solutions. We give topic-wise solutions for every question in Class 12 Maths NCERT Solutions and the Problems are solved by India’s best teachers. Students can prepare for CBSE Class 12 Maths NCERT Solutions Chapter 4 through this article for getting a better score in the CBSE exams. If the students practice the solutions multiple times, then it will be easier for them to solve the toughest problems that are appeared in the examinations. NCERT Solutions For Class 12 gives you the best results in CBSE board exams. You can clarify all doubts regarding this chapter 4 by simply downloading it.

Class 12 Maths NCERT Solutions Chapter 4 – Determinants

Name Of The Section	Topic Name
4	Determinants
4.1	Introduction
4.2	Determinant
4.3	Properties of Determinants
4.4	Area of Triangle
4.5	Adjoint and Inverse of a Matrix
4.6	Summary

NCERT Solutions For Class 12 Maths Chapter 4 Determinants Ex 4.1 – Introduction

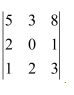
Question 1:
Evaluate the determinants in Exercises 1 and 2.

Answer:
= 2(−1) − 4(−5) = − 2 + 20 = 18

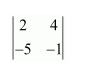
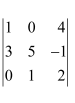
Question 2:
Evaluate the determinants in Exercises 1 and 2.
(i) 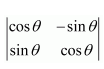(ii)
Answer:
(i) = (cos θ)(cos θ) − (−sin θ)(sin θ) = cos² θ+ sin² θ = 1
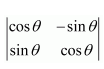
(ii)

Question 3:
If 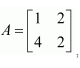then show that
Answer:
The given matrix is

Question 4:
If 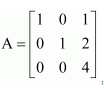then show that
Answer:
The given matrix is
It can be observed that in the first column, two entries are zero. Thus, we expand along the first column (C₁) for easier calculation.

From equations (i) and (ii), we have:

Hence, the given result is proved.

Question 5:

Evaluate the determinants
(i) 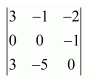(ii) (iii) (iv)
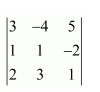
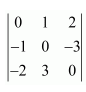
Answer:
(i) Let A=
It can be observed that in the second row, two entries are zero. Thus, we expand along the second row for easier calculation.

(ii) Let A=

By expanding along the first row, we have:

(iii) Let A=

By expanding along the first row, we have:

(iv) Let A=

By expanding along the first column, we have:

Question 6:
If 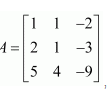find
Answer:
Let

By expanding along the first row, we have:

Question 7:

Find values of x, if

(i) 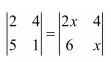(ii)

Answer:
(i)

(ii)

Question 8:
If

then x is equal to

(A) 6 (B) ±6 (C) −6 (D) 0
Answer:
Answer: B

Hence, the correct answer is B.

NCERT Solutions Class 12 Maths Chapter 4 Determinants Ex 4.2

Question 1:
Using the property of determinants and without expanding, prove that:

Answer:

Question 2:

Using the property of determinants and without expanding, prove that:

Answer:

Here, the two rows R₁ and R₃ are identical.

Δ = 0.

Question 3:

Using the property of determinants and without expanding, prove that:

Answer:

Question 4:

Using the property of determinants and without expanding, prove that:

Answer:

By applying C₃→ C₃ + C_2,we have:

Here, two columns C₁ and C₃are proportional.

Δ = 0.

Question 5:
Using the property of determinants and without expanding, prove that

Answer:

Applying R₂ → R₂ − R₃, we have:

Applying R₁ ↔R₃ and R₂ ↔R₃, we have:

Applying R₁→ R₁ − R₃, we have:

Applying R₁ ↔R₂ and R₂ ↔R₃, we have:

From (1), (2), and (3), we have:

Hence, the given result is proved.

Question 6:

By using properties of determinants, show that:

Answer:
We have,

Here, the two rows R₁ and R₃are identical.

∴Δ = 0.

Question 7:

By using properties of determinants, show that:

Answer:

Applying R₂→ R₂ + R₁ and R₃→ R₃ + R₁, we have:

Question 8:

By using properties of determinants, show that:
(i)
(ii)
Answer:
(i)

Applying R₁ → R₁ − R₃and R₂ → R₂ − R₃, we have:

Applying R₁ → R₁ + R₂, we have:

Expanding along C₁, we have:

Hence, the given result is proved.
(ii) Let

Applying C₁ → C₁ − C₃and C₂ → C₂ − C₃, we have:

Applying C₁ → C₁ + C₂, we have:

Expanding along C₁, we have:

Hence, the given result is proved.

Question 9:

By using properties of determinants, show that:

Answer:

Applying R₂ → R₂ − R₁and R₃ → R₃ − R₁, we have:

Applying R₃ → R₃ + R₂, we have:

Expanding along R₃, we have:

Hence, the given result is proved.

Question 10:

By using properties of determinants, show that:
(i)
(ii)
Answer:
(i)

Applying R₁ → R₁ + R₂+ R₃, we have:

Applying C₂ → C₂ − C₁, C₃ → C₃ − C₁, we have:

Expanding along C₃, we have:

Hence, the given result is proved.
(ii)

Applying R₁ → R₁ + R₂+ R₃, we have:

Applying C₂ → C₂ − C₁and C₃ → C₃ − C₁, we have:

Expanding along C₃, we have:

Hence, the given result is proved.

Question 11:

By using properties of determinants, show that:
(i)
(ii)
Answer:
(i)

Applying R₁ → R₁ + R₂+ R₃, we have:

Applying C₂ → C₂ − C₁, C₃ → C₃ − C₁, we have:

Expanding along C₃, we have:

Hence, the given result is proved.
(ii)

Applying C₁ → C₁ + C₂+ C₃, we have:

Applying R₂ → R₂ − R₁and R₃ → R₃ − R₁, we have:

Expanding along R₃, we have:

Hence, the given result is proved.

Question 12:

By using properties of determinants, show that:

Answer:

Applying R₁ → R₁ + R₂+ R₃, we have:

Applying C₂ → C₂ − C₁and C₃ → C₃ − C₁, we have:

Expanding along R₁, we have:

Hence, the given result is proved.

Question 13:

By using properties of determinants, show that:

Answer:

Applying R₁ → R₁ + bR₃and R₂ → R₂ − aR₃, we have:

Expanding along R₁, we have:

Question 14:

By using properties of determinants, show that:

Answer:

Taking out common factors a, b, and c from R₁, R₂, and R₃respectively, we have:

Applying R₂ → R₂ − R₁and R₃ → R₃ − R₁, we have:

Applying C₁ → aC₁, C₂→ bC_2,and C₃ → cC₃, we have:

Expanding along R₃, we have:

Hence, the given result is proved.

Question 15:

Choose the correct answer.
Let A be a square matrix of order 3 × 3, then is equal to
(A) (B) (C) (D)
Answer:
Answer: C
A is a square matrix of order 3 × 3.

Hence, the correct answer is C.

Question 16:

Which of the following is correct?

A. Determinant is a square matrix.

B. Determinant is a number associated to a matrix.

C. Determinant is a number associated to a square matrix.

D. None of these
Answer:

Answer: C
We know that to every square matrix, of order n. We can associate a number called the determinant of square matrix A, where

element of A.

Thus, the determinant is a number associated to a square matrix.

Hence, the correct answer is C.

NCERT Solutions For Class 12 Maths Chapter 4 Determinants Ex 4.3 Properties of Determinants

Question 1:

Find area of the triangle with vertices at the point given in each of the following:

(i) (1, 0), (6, 0), (4, 3) (ii) (2, 7), (1, 1), (10, 8)

(iii) (−2, −3), (3, 2), (−1, −8)
Answer:
(i) The area of the triangle with vertices (1, 0), (6, 0), (4, 3) is given by the relation,

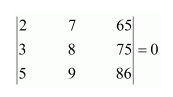
(ii) The area of the triangle with vertices (2, 7), (1, 1), (10, 8) is given by the relation,

(iii) The area of the triangle with vertices (−2, −3), (3, 2), (−1, −8)

is given by the relation,

Hence, the area of the triangle is

Question 2:

Show that points are collinear
Answer:

Area of ΔABC is given by the relation,

Thus, the area of the triangle formed by points A, B, and C is zero.

Hence, the points A, B, and C are collinear.

Question 3:

Find values of k if area of triangle is 4 square units and vertices are

(i) (k, 0), (4, 0), (0, 2) (ii) (−2, 0), (0, 4), (0, k)
Answer:

We know that the area of a triangle whose vertices are (x₁, y₁), (x₂, y₂), and

(x₃, y₃) is the absolute value of the determinant (Δ), where

It is given that the area of triangle is 4 square units.

∴Δ = ± 4.

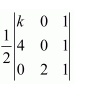
(i) The area of the triangle with vertices (k, 0), (4, 0), (0, 2) is given by the relation,
Δ =

∴−k + 4 = ± 4

When −k + 4 = − 4, k = 8.

When −k + 4 = 4, k = 0.

Hence, k = 0, 8.

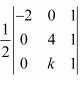
(ii) The area of the triangle with vertices (−2, 0), (0, 4), (0, k) is given by the relation,
Δ =

∴k − 4 = ± 4

When k − 4 = − 4, k = 0.

When k − 4 = 4, k = 8.

Hence, k = 0, 8.

Question 4:

(i) Find equation of line joining (1, 2) and (3, 6) using determinants

(ii) Find equation of line joining (3, 1) and (9, 3) using determinants
Answer:
(i) Let P (x, y) be any point on the line joining points A (1, 2) and B (3, 6). Then, the points A, B, and P are collinear. Therefore, the area of triangle ABP will be zero.

Hence, the equation of the line joining the given points is y = 2x.

(ii) Let P (x, y) be any point on the line joining points A (3, 1) and

B (9, 3). Then, the points A, B, and P are collinear. Therefore, the area of triangle ABP will be zero.

Hence, the equation of the line joining the given points is x − 3y = 0.

Question 5:

If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4). Then k is

A. 12 B. −2 C. −12, −2 D. 12, −2
Answer:

Answer: D

The area of the triangle with vertices (2, −6), (5, 4), and (k, 4) is given by the relation,

It is given that the area of the triangle is ±35.

Therefore, we have:

When 5 − k = −7, k = 5 + 7 = 12.

When 5 − k = 7, k = 5 − 7 = −2.

Hence, k = 12, −2.

The correct answer is D.

NCERT Solutions For Class 12 Maths Chapter 4 Determinants Ex 4.4 Area Of Triangle

Question 1:

Write Minors and Cofactors of the elements of the following determinants:
(i) (ii)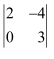
Answer:
(i) The given determinant is

Minor of element a_ij is M_ij.

∴M₁₁ = minor of element a₁₁= 3

M₁₂ = minor of element a₁₂= 0

M₂₁ = minor of element a₂₁= −4

M₂₂ = minor of element a₂₂= 2

Cofactor of a_ij is A_ij = (−1)^{i + j} M_ij.

∴A₁₁ = (−1)¹⁺¹ M₁₁ = (−1)² (3) = 3

A₁₂ = (−1)¹⁺² M₁₂ = (−1)³ (0) = 0

A₂₁ = (−1)²⁺¹ M₂₁ = (−1)³ (−4) = 4

A₂₂ = (−1)²⁺² M₂₂ = (−1)⁴ (2) = 2
(ii) The given determinant is

Minor of element a_ij is M_ij.

∴M₁₁ = minor of element a₁₁= d

M₁₂ = minor of element a₁₂= b

M₂₁ = minor of element a₂₁= c

M₂₂ = minor of element a₂₂= a

Cofactor of a_ij is A_ij = (−1)^{i + j} M_ij.

∴A₁₁ = (−1)¹⁺¹ M₁₁ = (−1)² (d) = d

A₁₂ = (−1)¹⁺² M₁₂ = (−1)³ (b) = −b

A₂₁ = (−1)²⁺¹ M₂₁ = (−1)³ (c) = −c

A₂₂ = (−1)²⁺² M₂₂ = (−1)⁴ (a) = a

Question 2:
(i) (ii)
Answer:
(i) The given determinant is

By the definition of minors and cofactors, we have:
M₁₁= minor of a₁₁=

M₁₂= minor of a₁₂=

M₁₃= minor of a₁₃=

M₂₁= minor of a₂₁=

M₂₂= minor of a₂₂=

M₂₃= minor of a₂₃=

M₃₁= minor of a₃₁=

M₃₂= minor of a₃₂=

A₁₁= cofactor of a₁₁= (−1)¹⁺¹ M₁₁ = 1

A₁₂= cofactor of a₁₂= (−1)¹⁺² M₁₂ = 0

A₁₃= cofactor of a₁₃= (−1)¹⁺³ M₁₃ = 0

A₂₁= cofactor of a₂₁= (−1)²⁺¹ M₂₁ = 0

A₂₂= cofactor of a₂₂= (−1)²⁺² M₂₂ = 1

A₂₃= cofactor of a₂₃= (−1)²⁺³ M₂₃ = 0

A₃₁= cofactor of a₃₁= (−1)³⁺¹ M₃₁ = 0

A₃₂= cofactor of a₃₂= (−1)³⁺² M₃₂ = 0

A₃₃= cofactor of a₃₃= (−1)³⁺³ M₃₃ = 1
(ii) The given determinant is

By definition of minors and cofactors, we have:
M₁₁= minor of a₁₁=

M₁₂= minor of a₁₂=

M₁₃= minor of a₁₃=

M₂₁= minor of a₂₁=

M₂₂= minor of a₂₂=

M₂₃= minor of a₂₃=

M₃₁= minor of a₃₁=

M₃₂= minor of a₃₂=

M₃₃= minor of a₃₃=

A₁₁= cofactor of a₁₁= (−1)¹⁺¹ M₁₁ = 11

A₁₂= cofactor of a₁₂= (−1)¹⁺² M₁₂ = −6

A₁₃= cofactor of a₁₃= (−1)¹⁺³ M₁₃ = 3

A₂₁= cofactor of a₂₁= (−1)²⁺¹ M₂₁ = 4

A₂₂= cofactor of a₂₂= (−1)²⁺² M₂₂ = 2

A₂₃= cofactor of a₂₃= (−1)²⁺³ M₂₃ = −1

A₃₁= cofactor of a₃₁= (−1)³⁺¹ M₃₁ = −20

A₃₂= cofactor of a₃₂= (−1)³⁺² M₃₂ = 13

A₃₃= cofactor of a₃₃= (−1)³⁺³ M₃₃ = 5

Question 3:
Using Cofactors of elements of the second row, evaluate
Answer:
The given determinant is

We have:
M₂₁=
∴A₂₁= cofactor of a₂₁= (−1)²⁺¹ M₂₁ = 7
M₂₂=

∴A₂₂= cofactor of a₂₂= (−1)²⁺² M₂₂ = 7
M₂₃=

∴A₂₃= cofactor of a₂₃= (−1)²⁺³ M₂₃ = −7

We know that Δ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.

∴Δ = a₂₁A₂₁ + a₂₂A₂₂ + a₂₃A₂₃ = 2(7) + 0(7) + 1(−7) = 14 − 7 =7

Question 4:
Using Cofactors of elements of third column, evaluate

Answer:
The given determinant is

We have:
M₁₃=
M₂₃=
M₃₃=

∴A₁₃= cofactor of a₁₃= (−1)¹⁺³ M₁₃ = (z − y)

A₂₃= cofactor of a₂₃= (−1)²⁺³ M₂₃ = − (z − x) = (x − z)

A₃₃= cofactor of a₃₃= (−1)³⁺³ M₃₃ = (y − x)

We know that Δ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.

Hence Δ=(x-y)(y-z)(z-x)

Question 5:
If 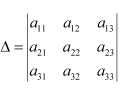and A_ij is Cofactors of a_ij, then value of Δ is given by

Answer:

Answer: D

We know that:

Δ = Sum of the product of the elements of a column (or a row) with their corresponding cofactors

∴Δ = a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

Hence, the value of Δ is given by the expression given in alternative D.

The correct answer is D.

NCERT Solutions For Class 12 Maths Chapter 4 Determinants Ex 4.5 Adjoint and Inverse of a Matrix

Question 1:

Find adjoint of each of the matrices.

Answer:

Question 2:

Find adjoint of each of the matrices.

Answer:

Question 3:
Verify A (adj A) = (adj A) A =

Answer:
A=

Question 4:
Verify A (adj A) = (adj A) A =

Answer:

Question 5:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 6:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 7:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 8:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 9:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 10:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 11:

Find the inverse of each of the matrices (if it exists).

Answer:

Question 12:
Let 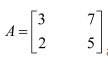and Verify that
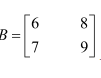
Answer:

From (1) and (2), we have:

(AB)⁻¹ = B⁻¹A⁻¹

Hence, the given result is proved.

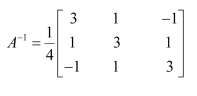
Question 13:
If 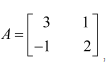show that Hence find
Answer:

Question 14:
For the matrix 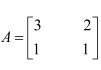find the numbers a and b such that A² + aA + bI = O.
Answer:
We have:
Comparing the corresponding elements of the two matrices, we have:

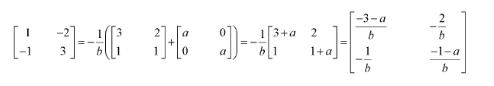
Hence, −4 and 1 are the required values of a and b respectively.

Question 15:
For the matrix 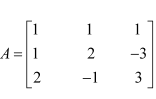show that A³ − 6A² + 5A + 11 I = O. Hence, find A^−1.
Answer:

From equation (1), we have:

Question 16:
If 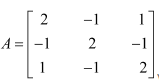verify that A³ − 6A² + 9A − 4I = O and hence find A⁻¹
Answer:

From equation (1), we have:

Question 17:
Let A be a nonsingular square matrix of order 3 × 3. Then is equal to
(A) (B) (C) (D)
Answer:

Answer: B

We know that

Hence, the correct answer is B.

Question 18:
If A is an invertible matrix of order 2, then det (A⁻¹) is equal to A. det (A) B 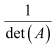C. 1 D. 0
Answer:
Since A is an invertible matrix,

Hence, the correct answer is B.

NCERT Solutions For Class 12 Maths Chapter 4 Determinants Ex 4.6 Summary

Question 1:

Examine the consistency of the system of equations.

x + 2y = 2

2x + 3y = 3
Answer:

The given system of equations is:

x + 2y = 2

2x + 3y = 3

The given system of equations can be written in the form of AX = B, where

∴ A is non-singular.

Therefore, A⁻¹ exists.

Hence, the given system of equations is consistent.

Question 2:

Examine the consistency of the system of equations.

2x − y = 5

x + y = 4
Answer:

The given system of equations is:

2x − y = 5

x + y = 4

The given system of equations can be written in the form of AX = B, where

∴ A is non-singular.

Therefore, A⁻¹ exists.

Hence, the given system of equations is consistent.

Question 3:

Examine the consistency of the system of equations.

x + 3y = 5

2x + 6y = 8
Answer:

The given system of equations is:

x + 3y = 5

2x + 6y = 8

The given system of equations can be written in the form of AX = B, where

∴ A is a singular matrix.

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

Question 4:

Examine the consistency of the system of equations.

x + y + z = 1

2x + 3y + 2z = 2

ax + ay + 2az = 4
Answer:

The given system of equations is:

x + y + z = 1

2x + 3y + 2z = 2

ax + ay + 2az = 4

This system of equations can be written in the form AX = B, where

∴ A is non-singular.

Therefore, A⁻¹ exists.

Hence, the given system of equations is consistent.

Question 5:

Examine the consistency of the system of equations.

3x − y − 2z = 2

2y − z = −1

3x − 5y = 3
Answer:

The given system of equations is:

3x − y − 2z = 2

2y − z = −1

3x − 5y = 3

This system of equations can be written in the form of AX = B, where

∴ A is a singular matrix.

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

Question 6:

Examine the consistency of the system of equations.

5x − y + 4z = 5

2x + 3y + 5z = 2

5x − 2y + 6z = −1
Answer:

The given system of equations is:

5x − y + 4z = 5

2x + 3y + 5z = 2

5x − 2y + 6z = −1

This system of equations can be written in the form of AX = B, where

∴ A is non-singular.

Therefore, A⁻¹ exists.

Hence, the given system of equations is consistent.

Question 7:

Solve system of linear equations, using matrix method.

Answer:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 8:

Solve system of linear equations, using matrix method.
2x-y=-2
3x+4y=3
Answer:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 9:

Solve system of linear equations, using matrix method.
4x-3y=3
3x-5y=7
Answer:

The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 10:

Solve system of linear equations, using matrix method.

5x + 2y = 3

3x + 2y = 5
Answer:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 11:

Solve system of linear equations, using matrix method.

Answer:

The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 12:

Solve system of linear equations, using matrix method.

x − y + z = 4

2x + y − 3z = 0

x + y + z = 2
Answer:

The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 13:

Solve system of linear equations, using matrix method.

2x + 3y + 3z = 5

x − 2y + z = −4

3x − y − 2z = 3
Answer:

The given system of equations can be written in the form AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 14:

Solve system of linear equations, using matrix method.

x − y + 2z = 7

3x + 4y − 5z = −5

2x − y + 3z = 12
Answer:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Question 15:
If find A⁻¹. Using A⁻¹ solve the system of equations

Answer:

Now, the given system of equations can be written in the form of AX = B, where

Question 16:

The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg

wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70.

Find cost of each item per kg by matrix method.
Answer:

Let the cost of onions, wheat, and rice per kg be Rs x, Rs y,and Rs z respectively.

Then, the given situation can be represented by a system of equations as

This system of equations can be written in the form of AX = B, where

Now,

X = A⁻¹ B

Hence, the cost of onions is Rs 5 per kg, the cost of wheat is Rs 8 per kg, and the cost of rice is Rs 8 per kg.

NCERT Solutions For Class 12 Maths Chapter 4 Determinants Miscellaneous Solutions

Question 1:
Prove that the determinant 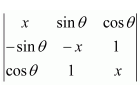is independent of θ.
Answer:
Δ=

Question 2:

Without expanding the determinant, prove that

Answer:

Hence, the given result is proved.

Question 3:
Evaluate
Answer:
Δ=

Expanding along C₃, we have:

Question 4:
If a, b and c are real numbers, and
Show that either a + b + c = 0 or a = b = c.
Answer:

Expanding along R₁, we have:

Hence, if Δ = 0, then either a + b + c = 0 or a = b = c.

Question 5:
Solve the equations
Answer:

Question 6:
Prove that
Answer:

Expanding along R₃, we have:

Hence, the given result is proved.

Question 7:
If
Answer:
We know that

Question 8:
Let 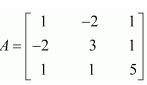verify that
(i)
(ii)
Answer:

(i)

We have,

(ii)

Question 9:
Evaluate
Answer:
Δ=

Expanding along R₁, we have:

Question 10:
Evaluate
Answer:

Expanding along C₁, we have:
Δ=1(xy-0)=xy

Question 11:

Using properties of determinants, prove that:

Answer:

Expanding along R₃, we have:

Hence, the given result is proved.

Question 12:

Using properties of determinants, prove that:

Answer:

Expanding along R₃, we have:

Hence, the given result is proved.

Question 13:

Using properties of determinants, prove that:

Answer:

Expanding along C₁, we have:

Hence, the given result is proved.

Question 14:

Using properties of determinants, prove that:

Answer:

Expanding along C₁, we have:

Hence, the given result is proved.

Question 15:

Using properties of determinants, prove that:

Answer:

Hence, the given result is proved.

Question 16:

Solve the system of the following equations

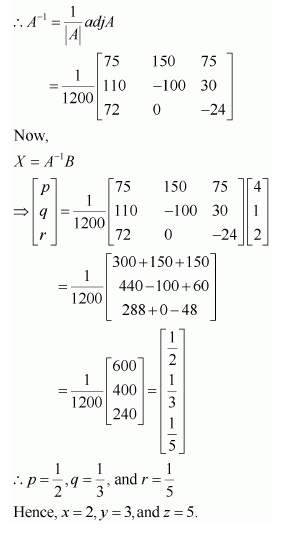
Answer:
Let

Then the given system of equations is as follows:

This system can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Now,

A₁₁ = 75, A₁₂ = 110, A₁₃ = 72

A₂₁ = 150, A₂₂ = −100, A₂₃ = 0

A₃₁ = 75, A₃₂ = 30, A₃₃ = − 24

Question 17:

Choose the correct answer.

If a, b, c, are in A.P., then the determinant

A. 0 B. 1 C. x D. 2x
Answer:

Answer: A

Here, all the elements of the first row (R₁) are zero.

Hence, we have Δ = 0.

The correct answer is A.

Question 18:

Choose the correct answer.

If x, y, z are nonzero real numbers, then the inverse of matrix
is
(A) (B) (C) (D)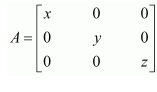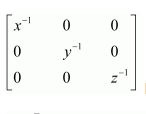
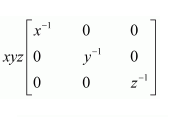
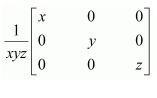
Answer:
Answer: A

The correct answer is A.

Question 19:

Choose the correct answer.
Let 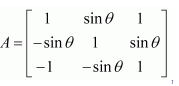where 0 ≤ θ≤ 2π, then

A. Det (A) = 0

B. Det (A) ∈ (2, ∞)

C. Det (A) ∈ (2, 4)

D. Det (A)∈ [2, 4] Answer:

Answer: D

Now, 0≤θ≤2π

⇒-1≤sinθ≤1
The correct answer is D.