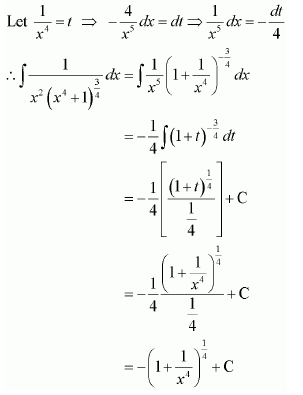
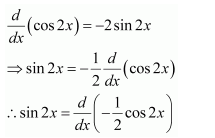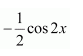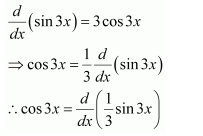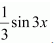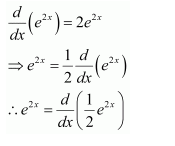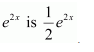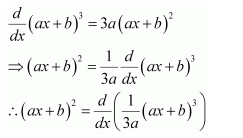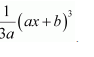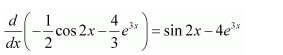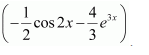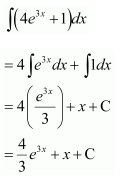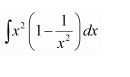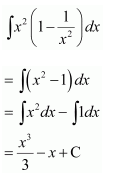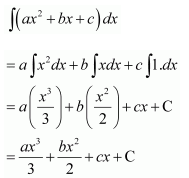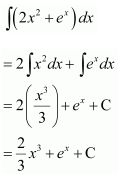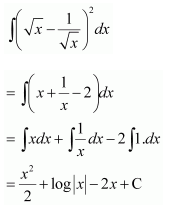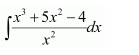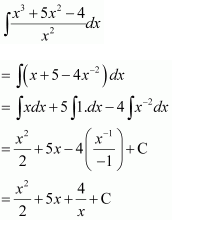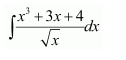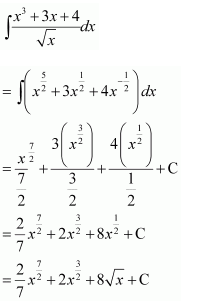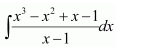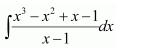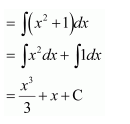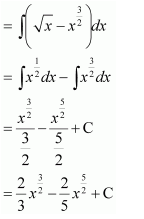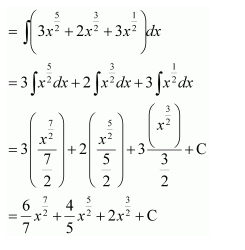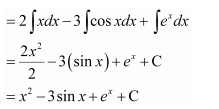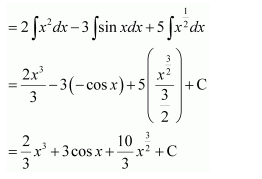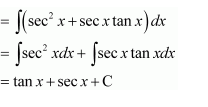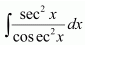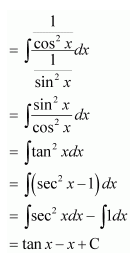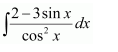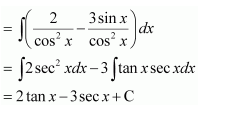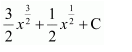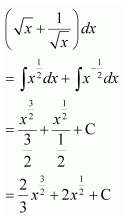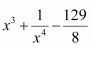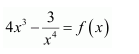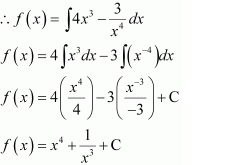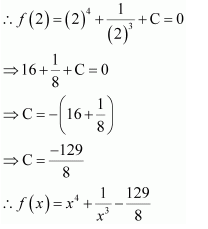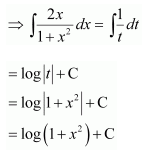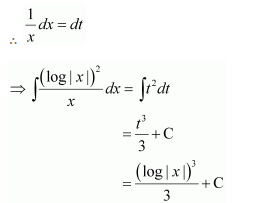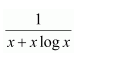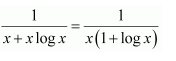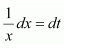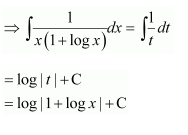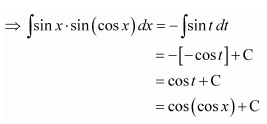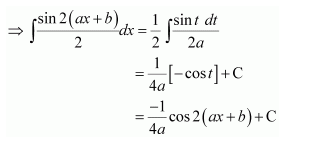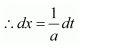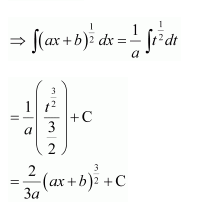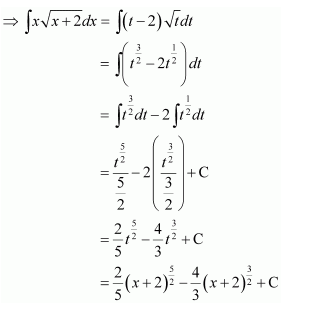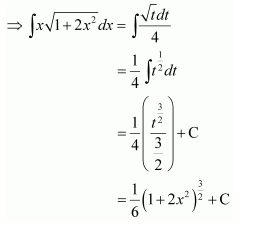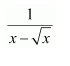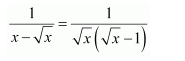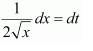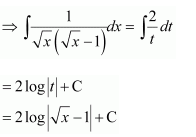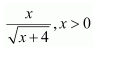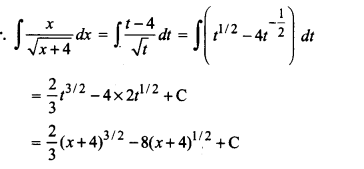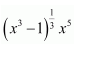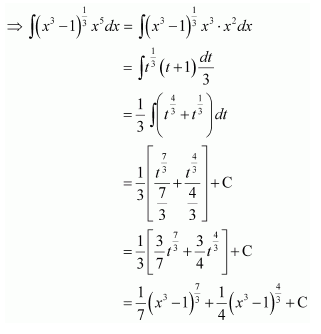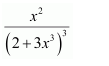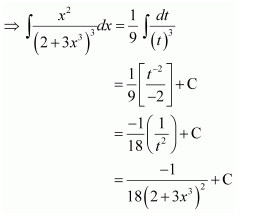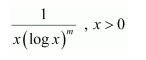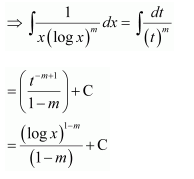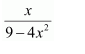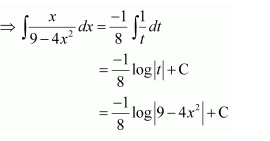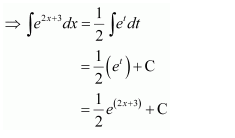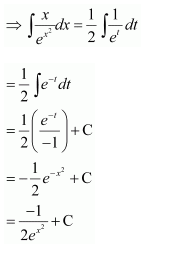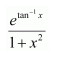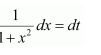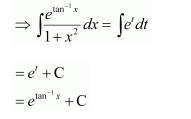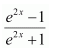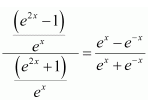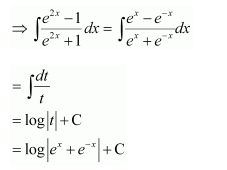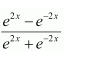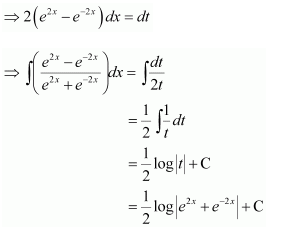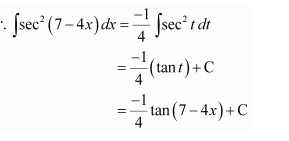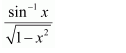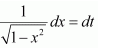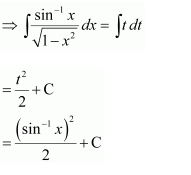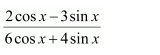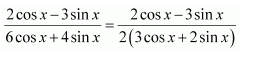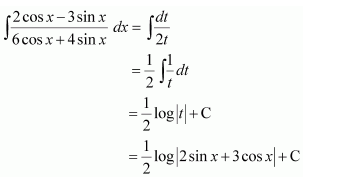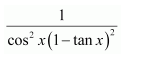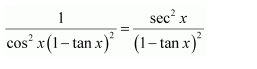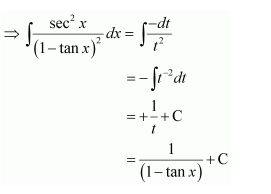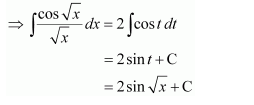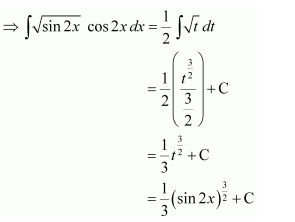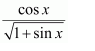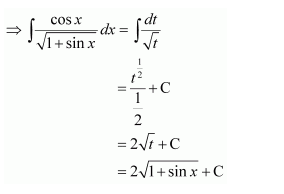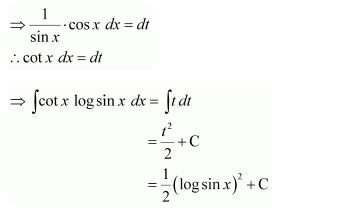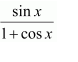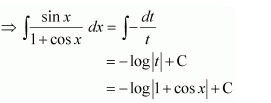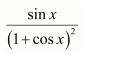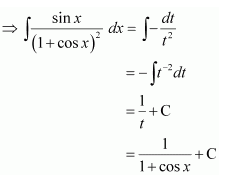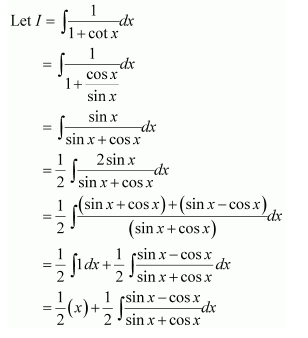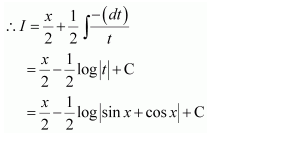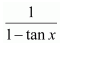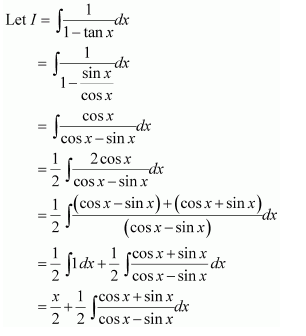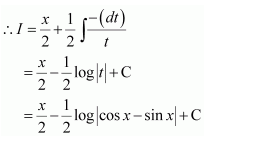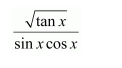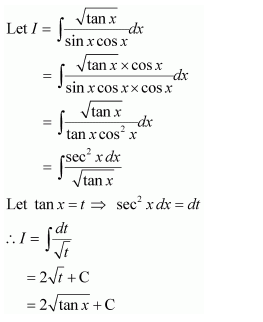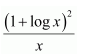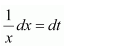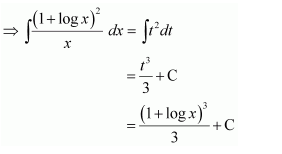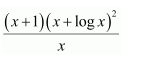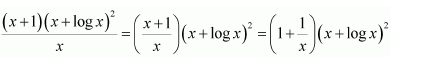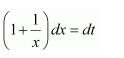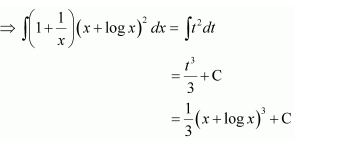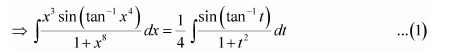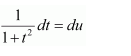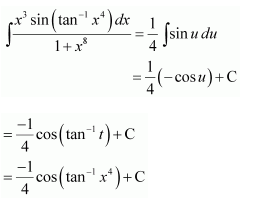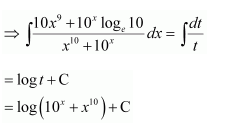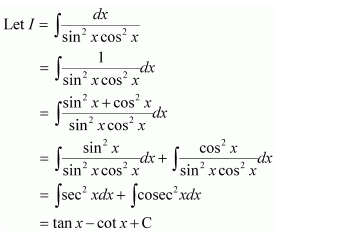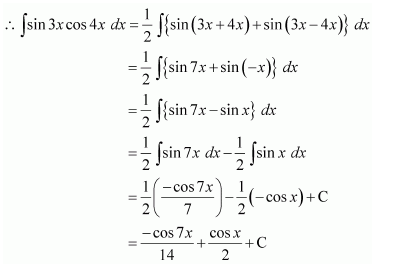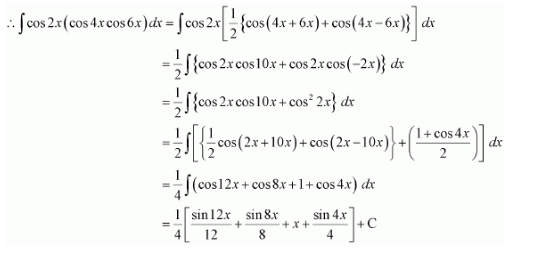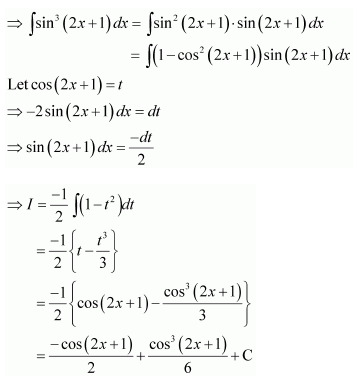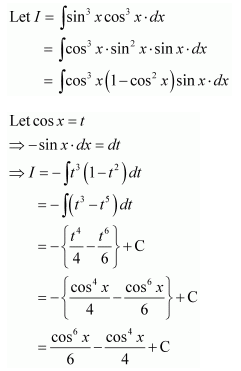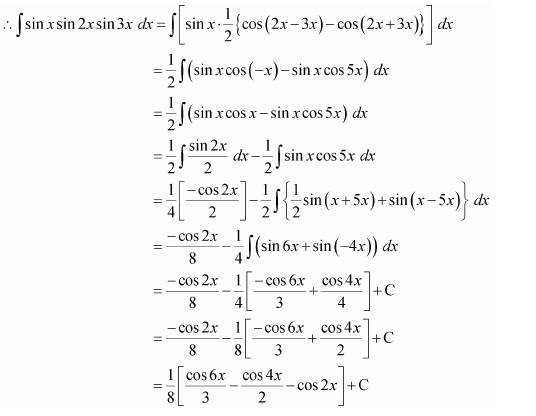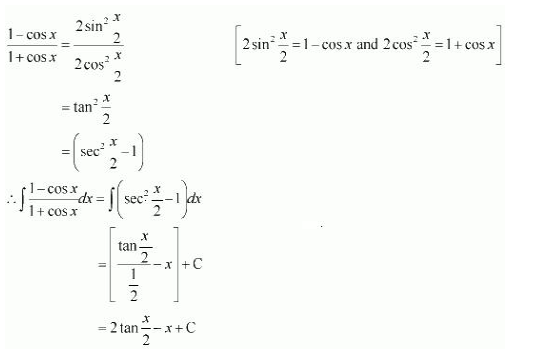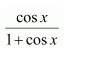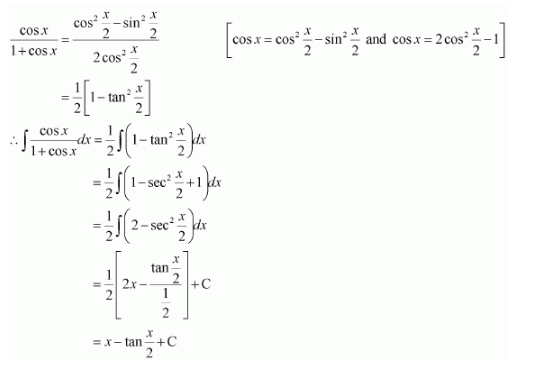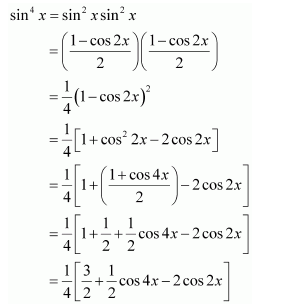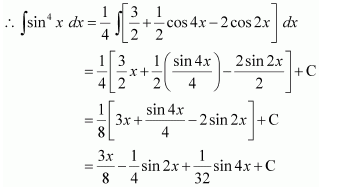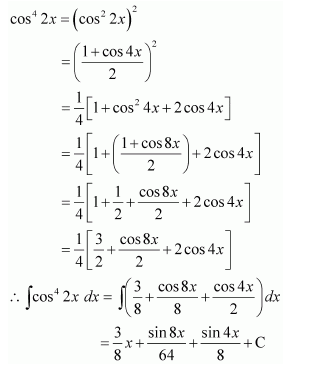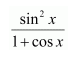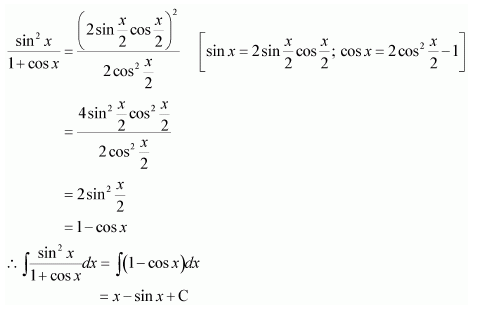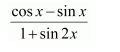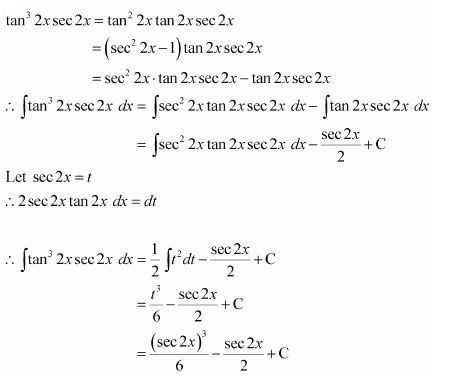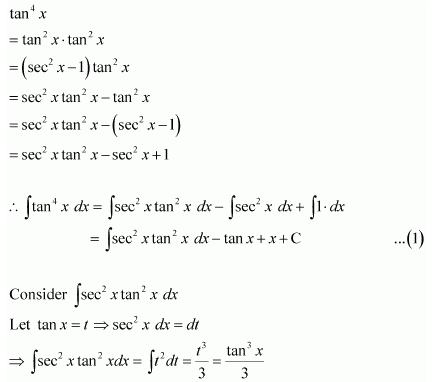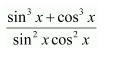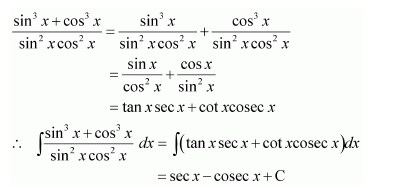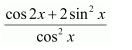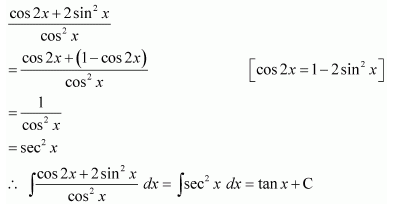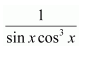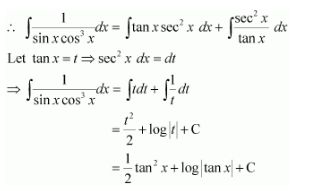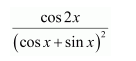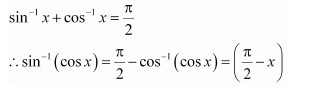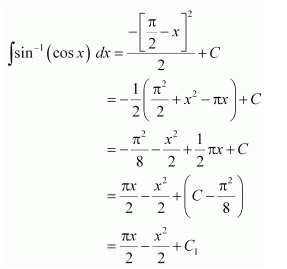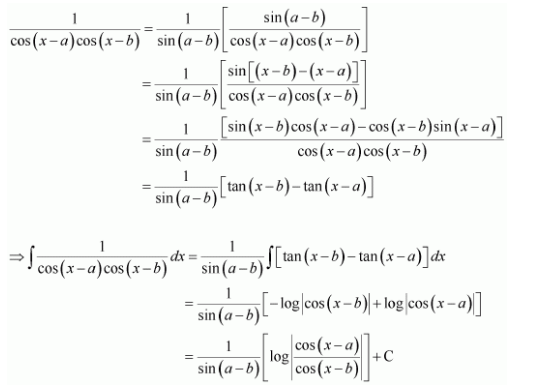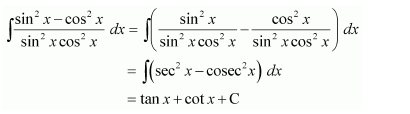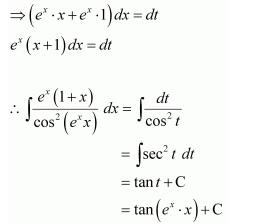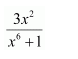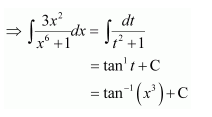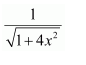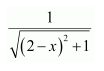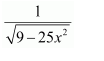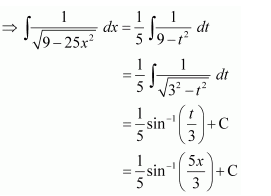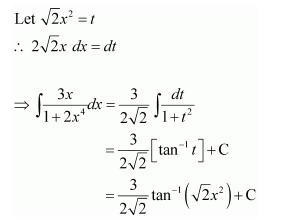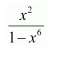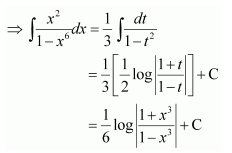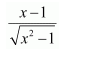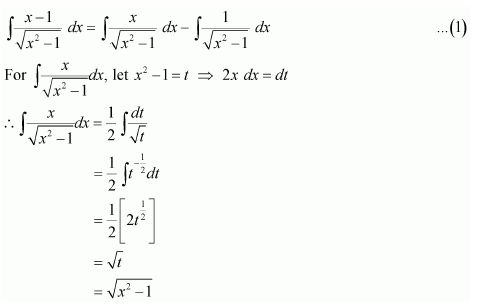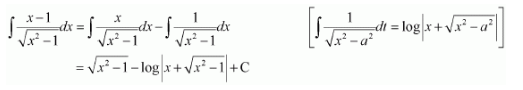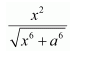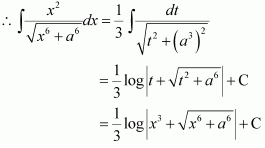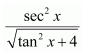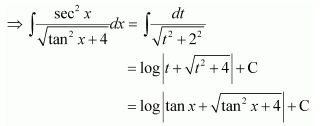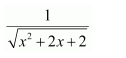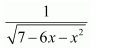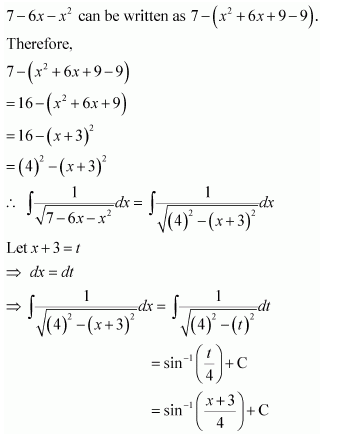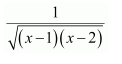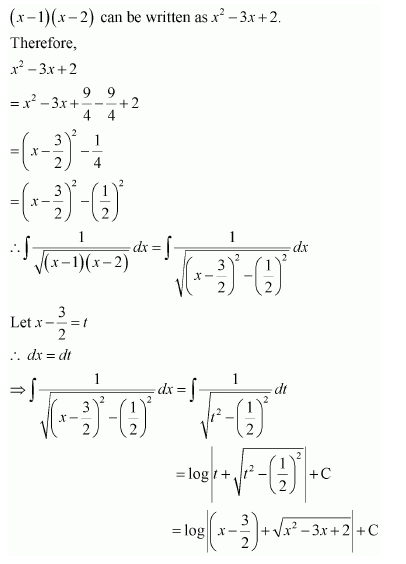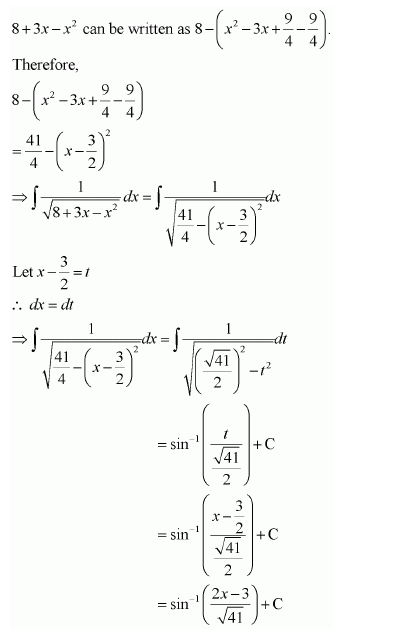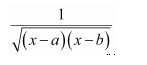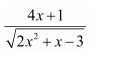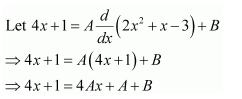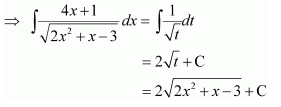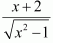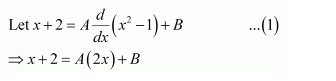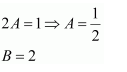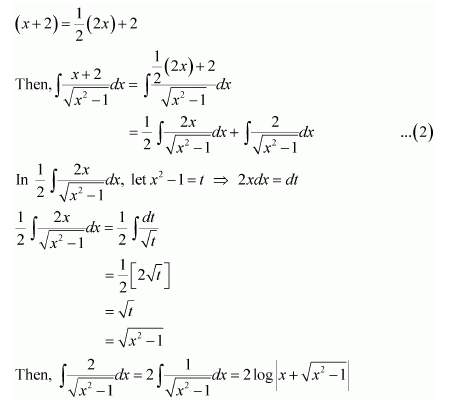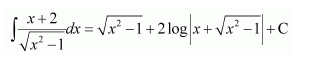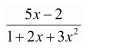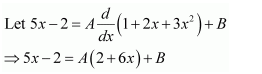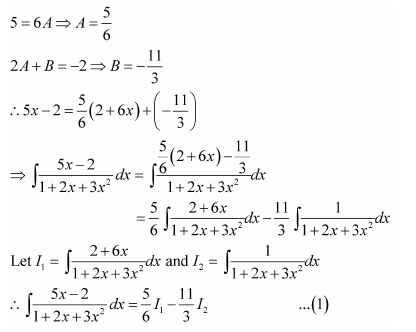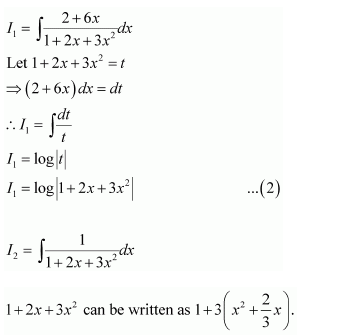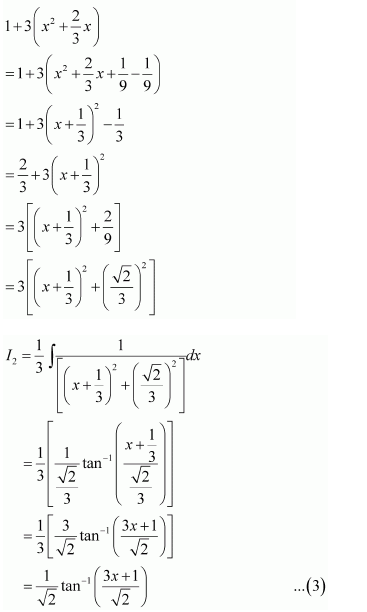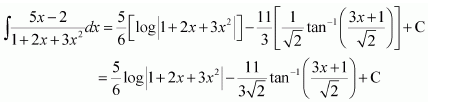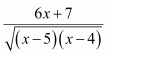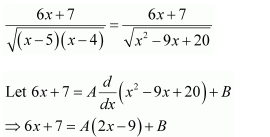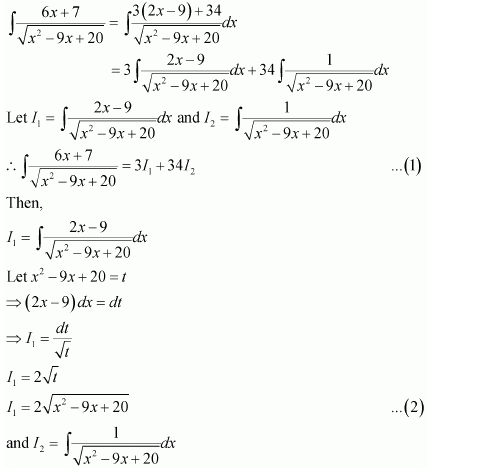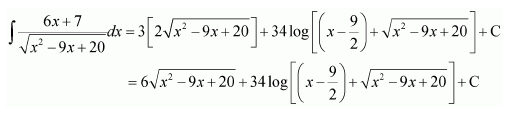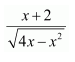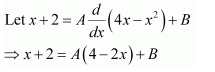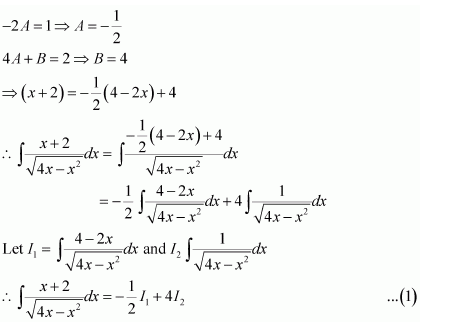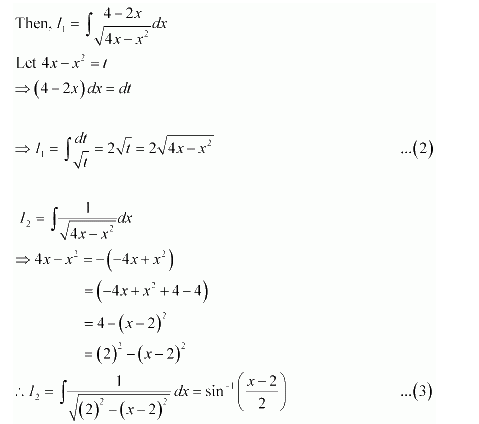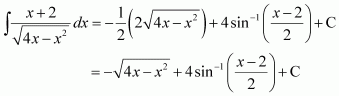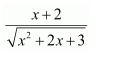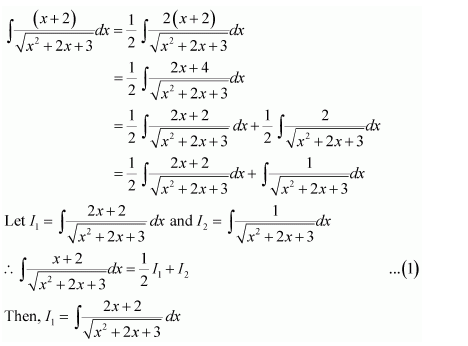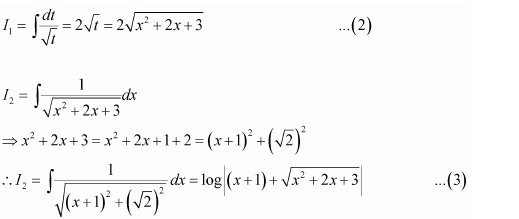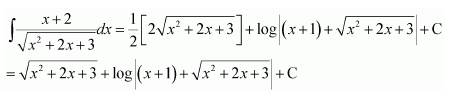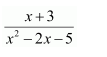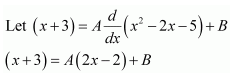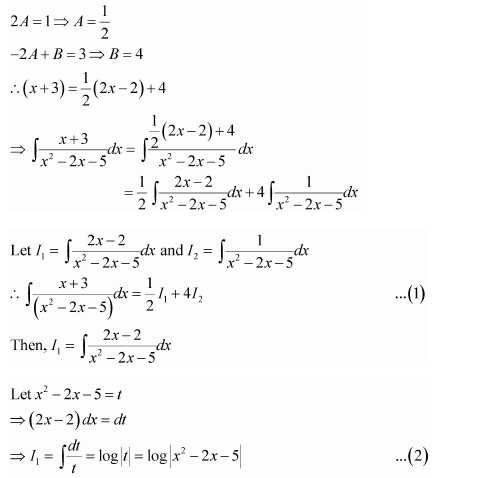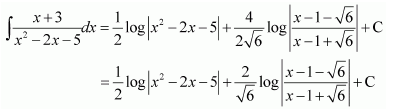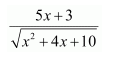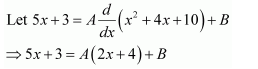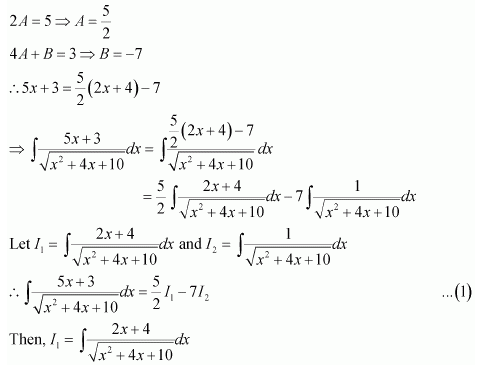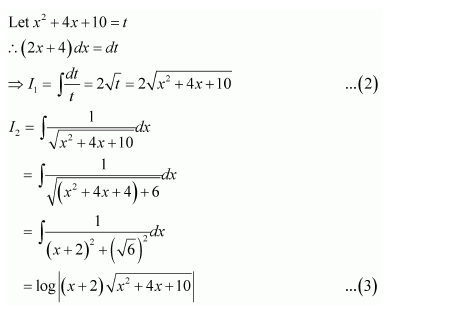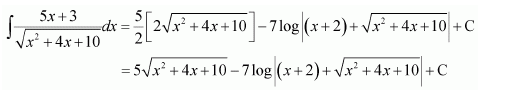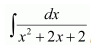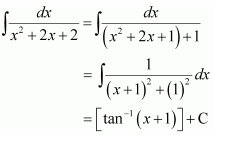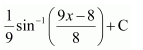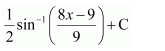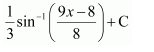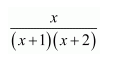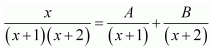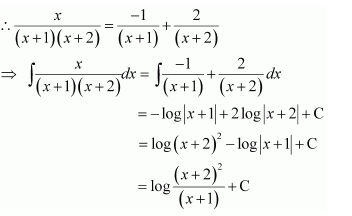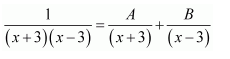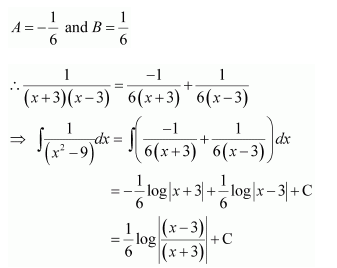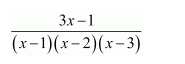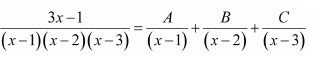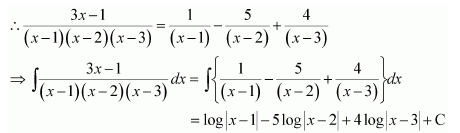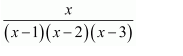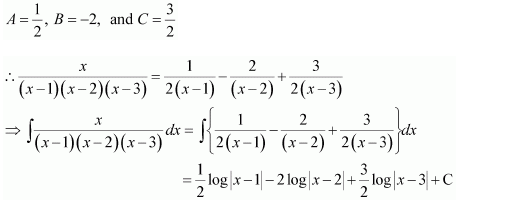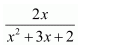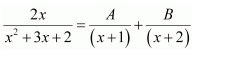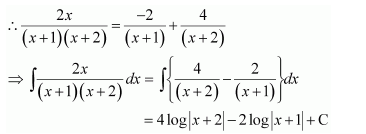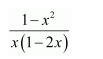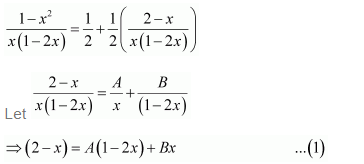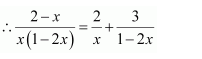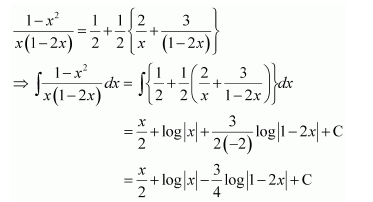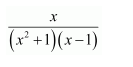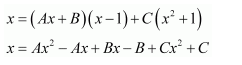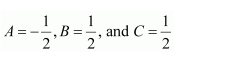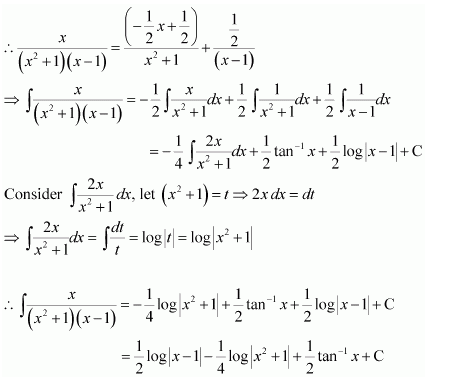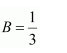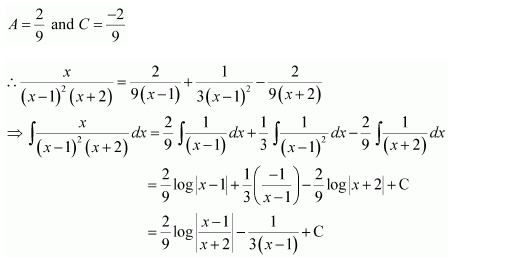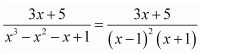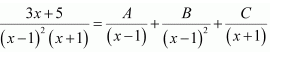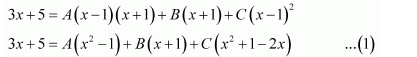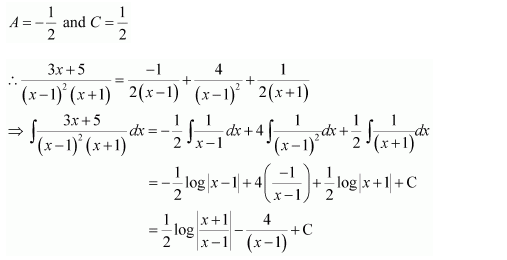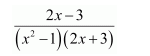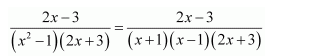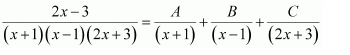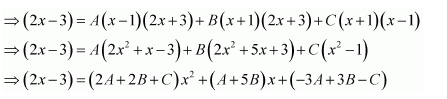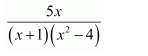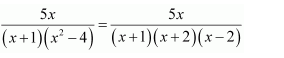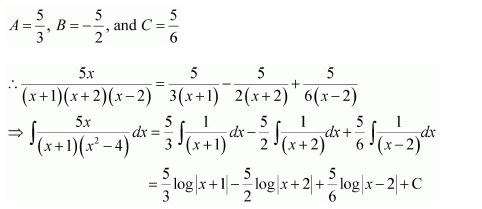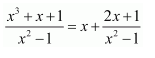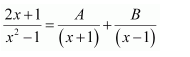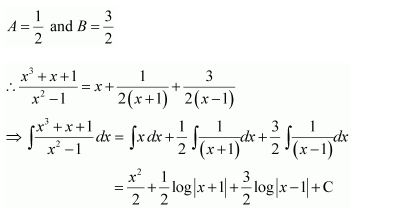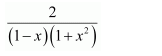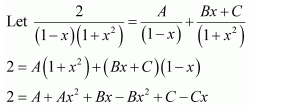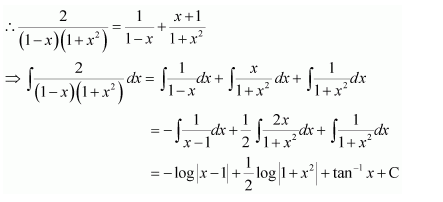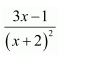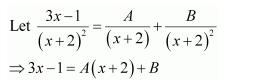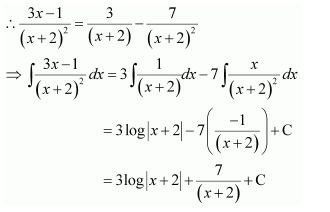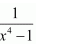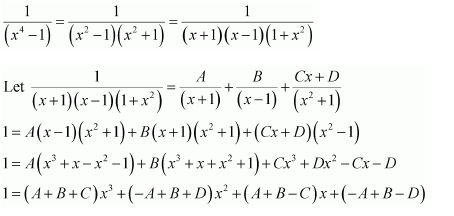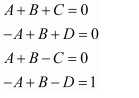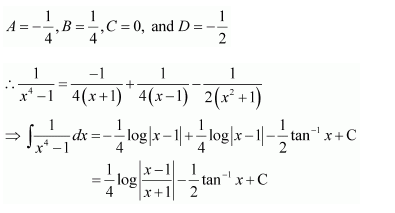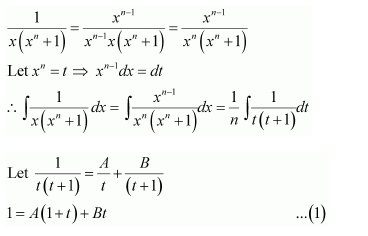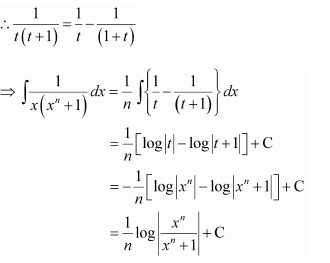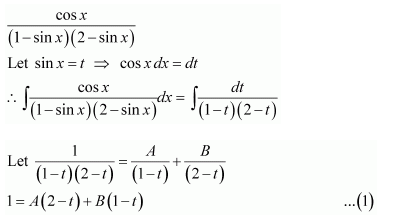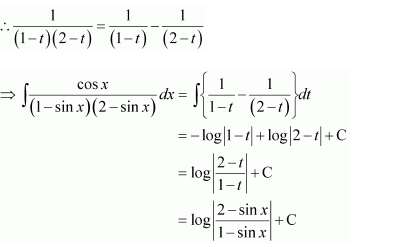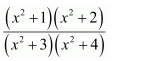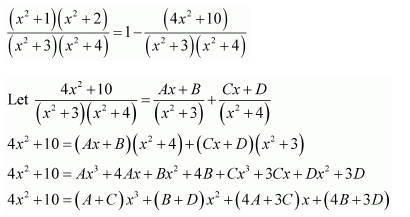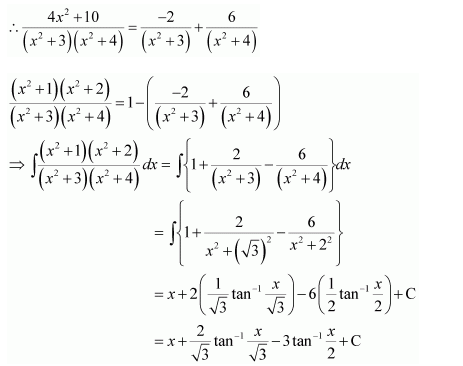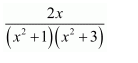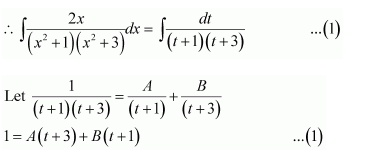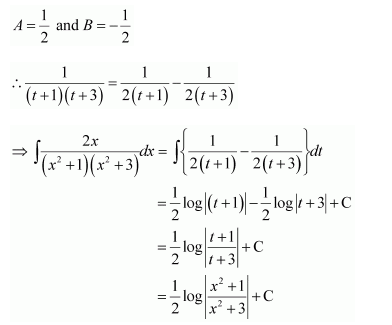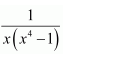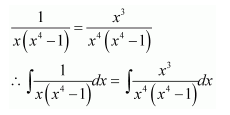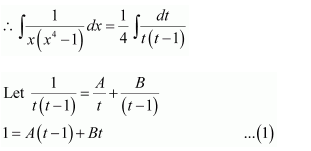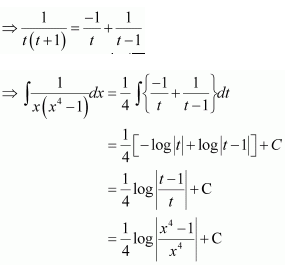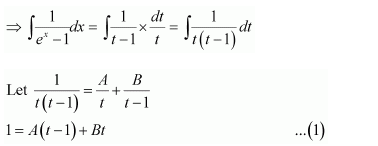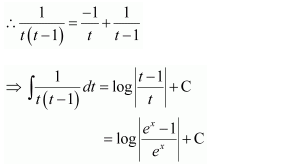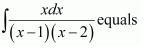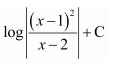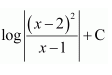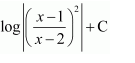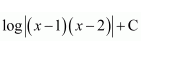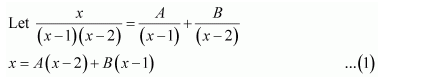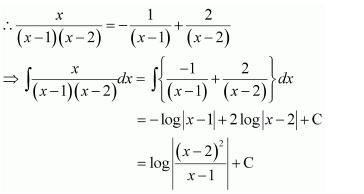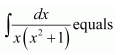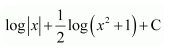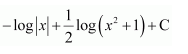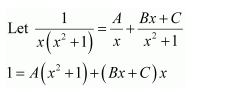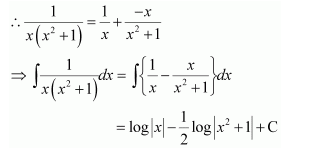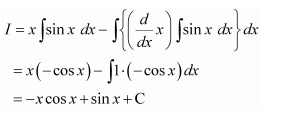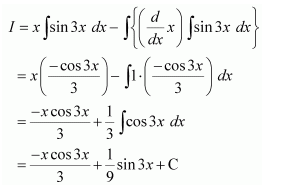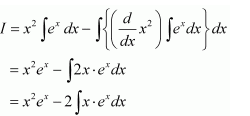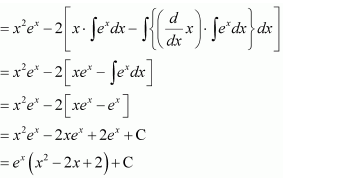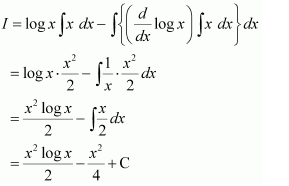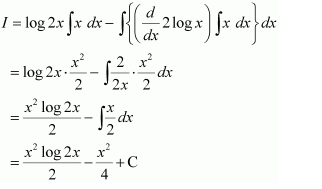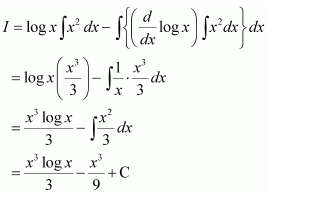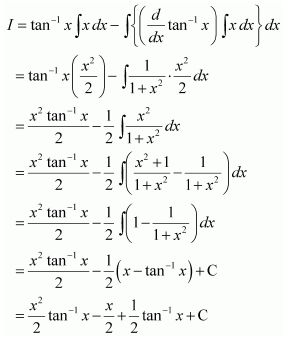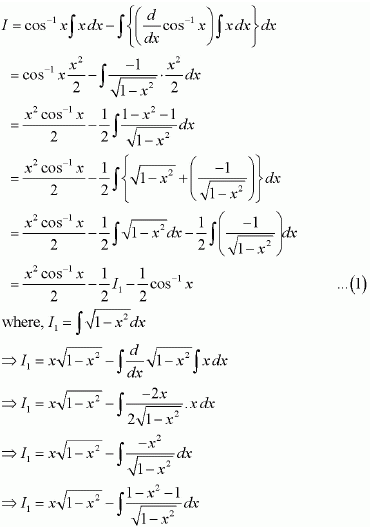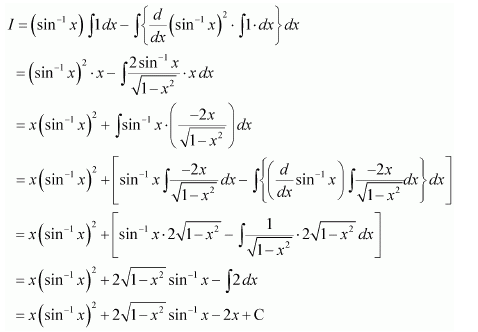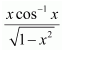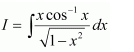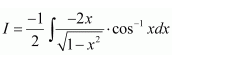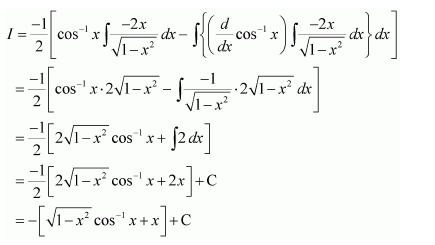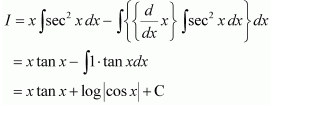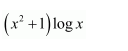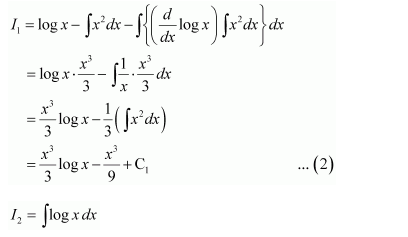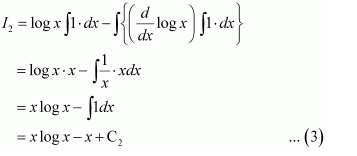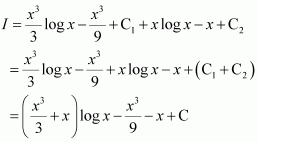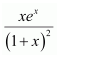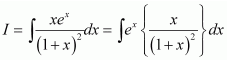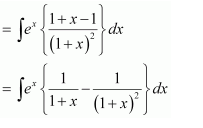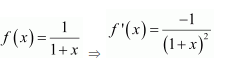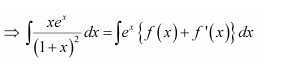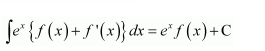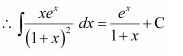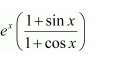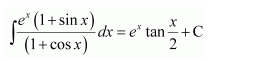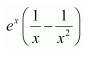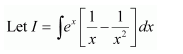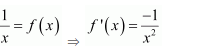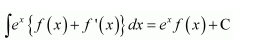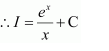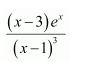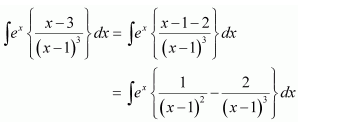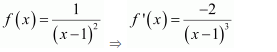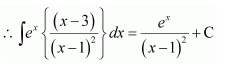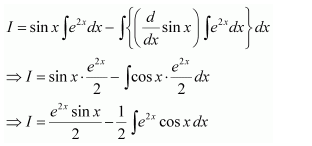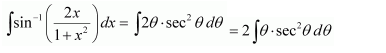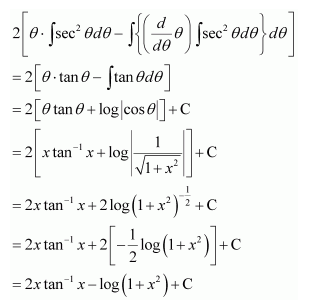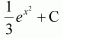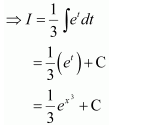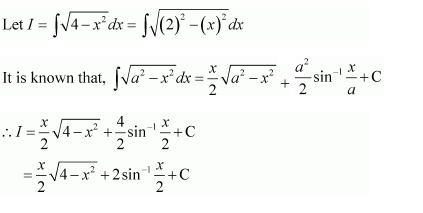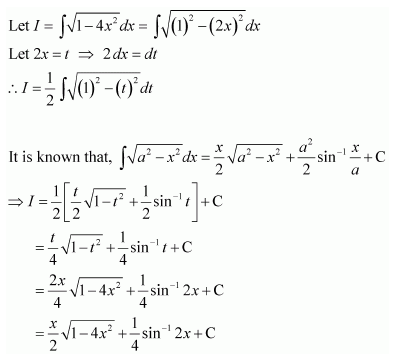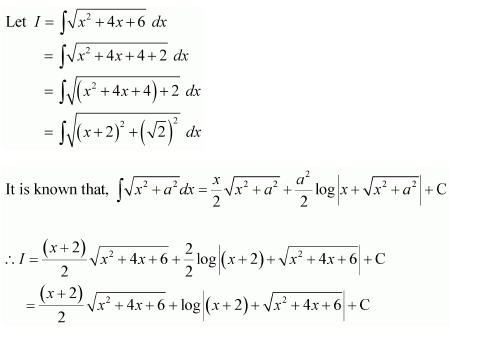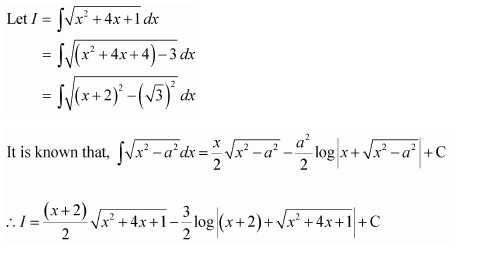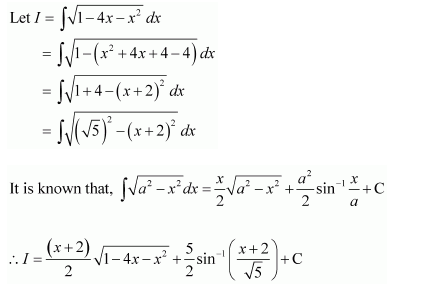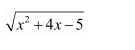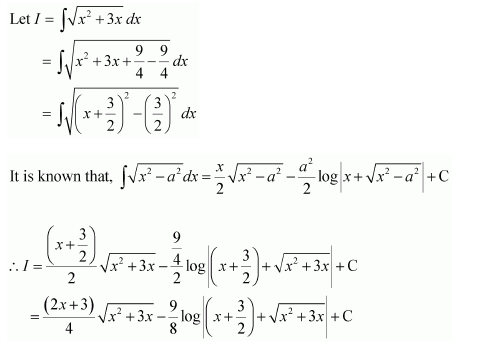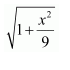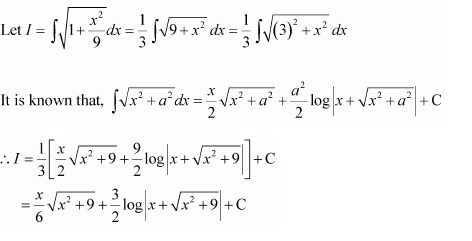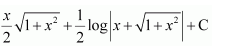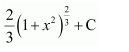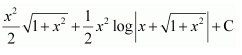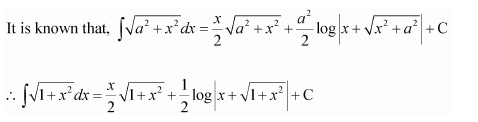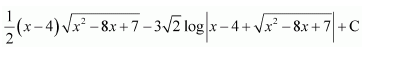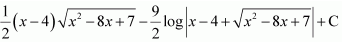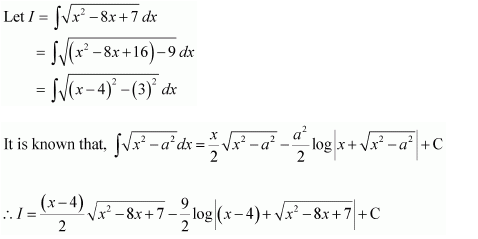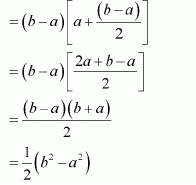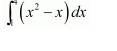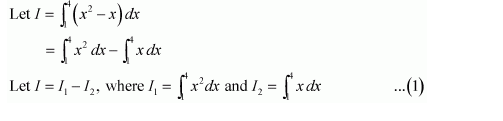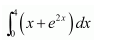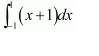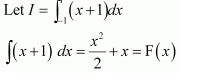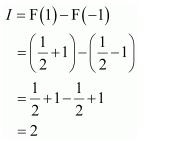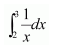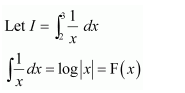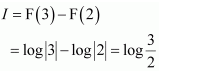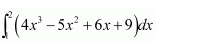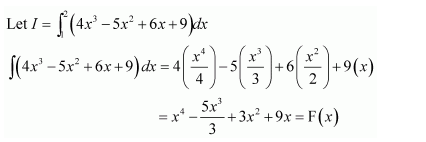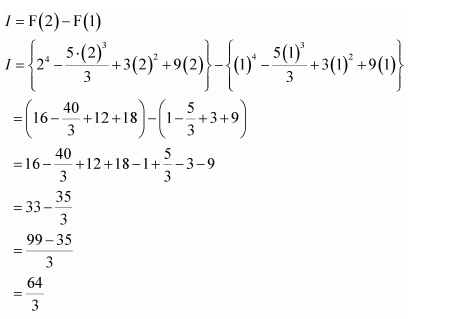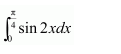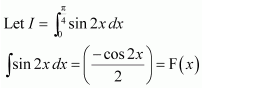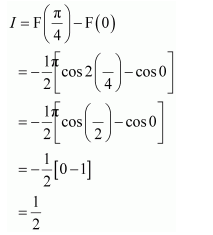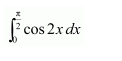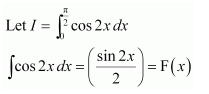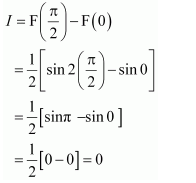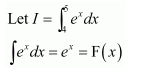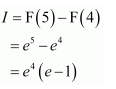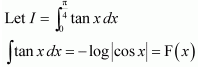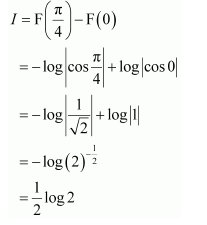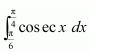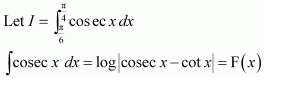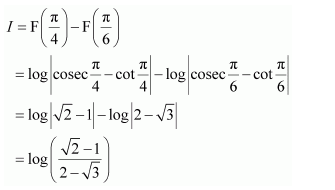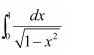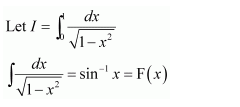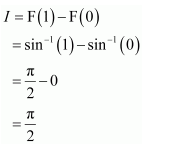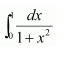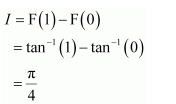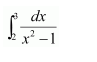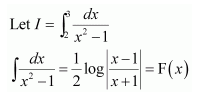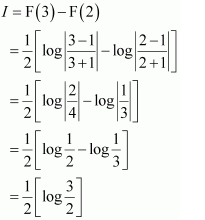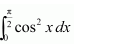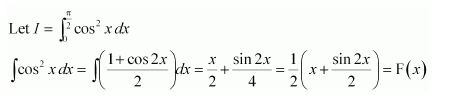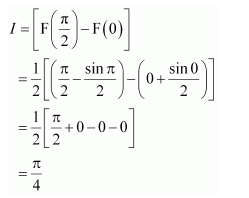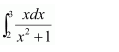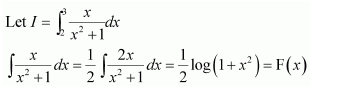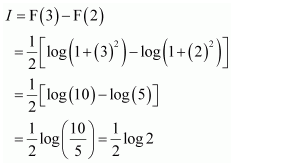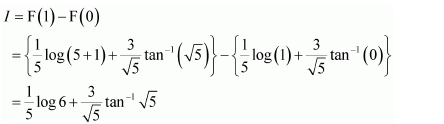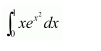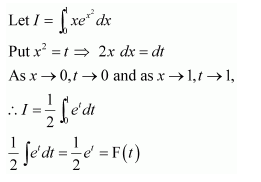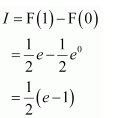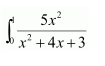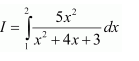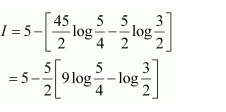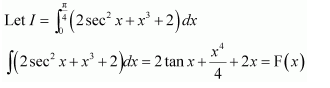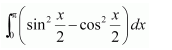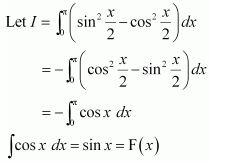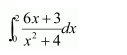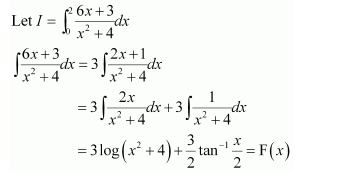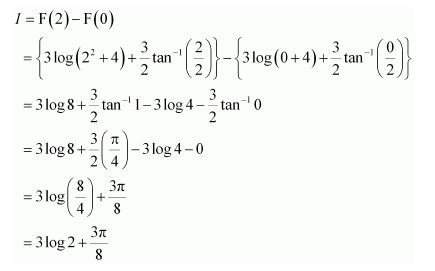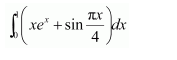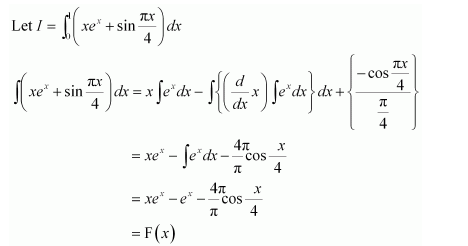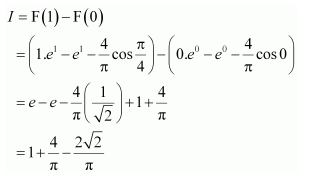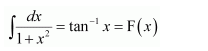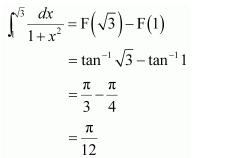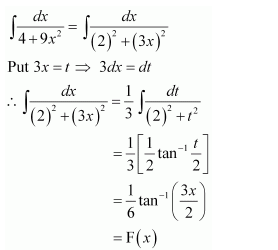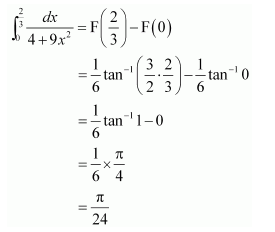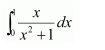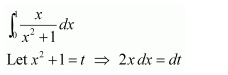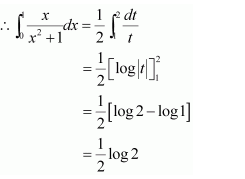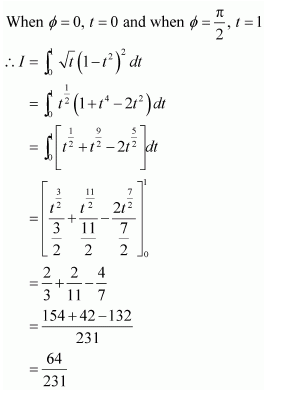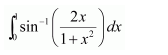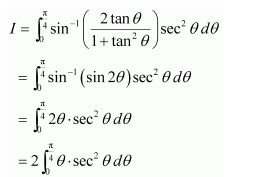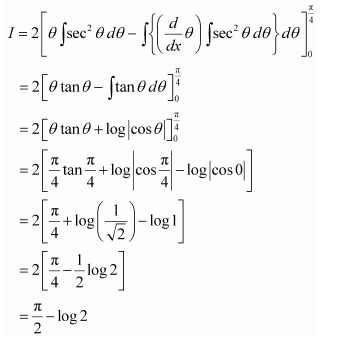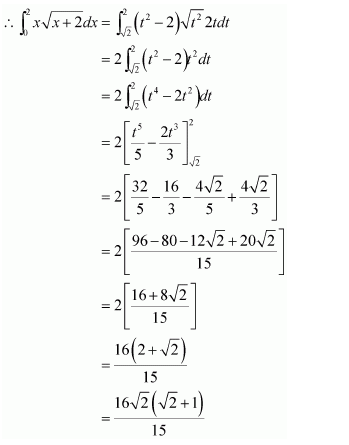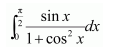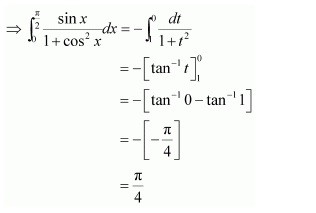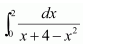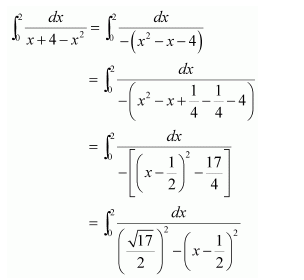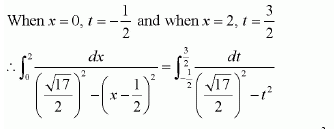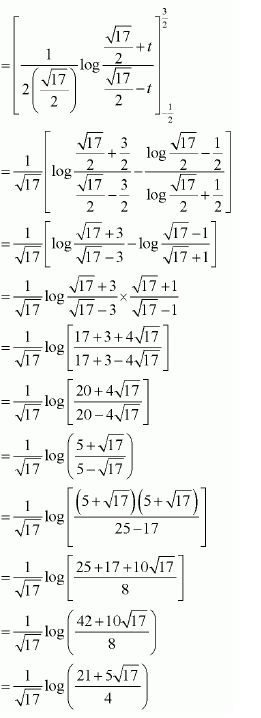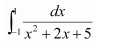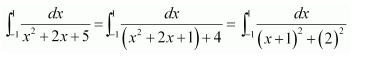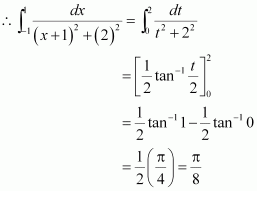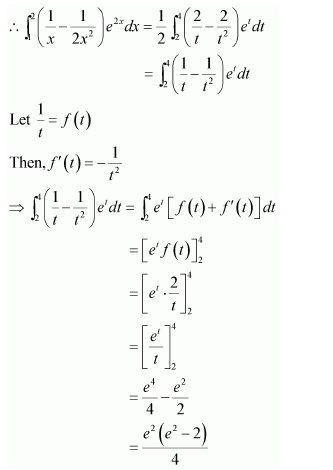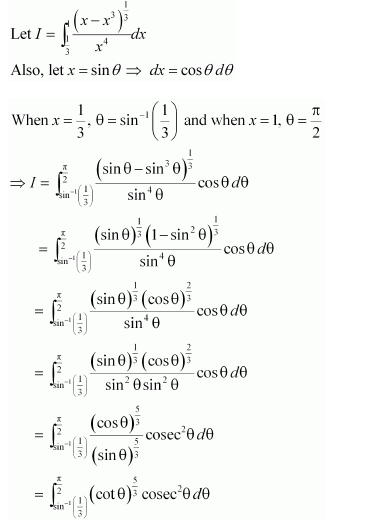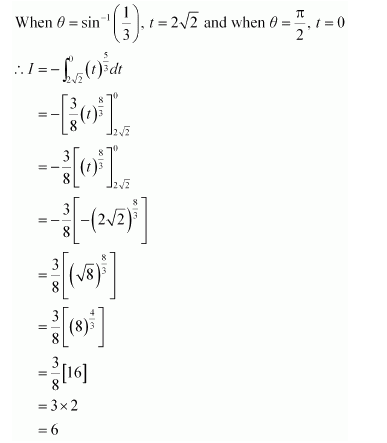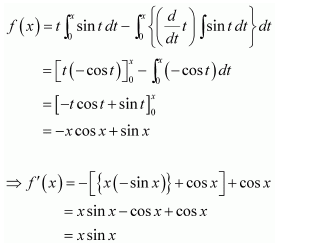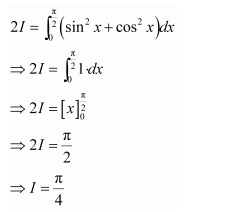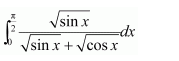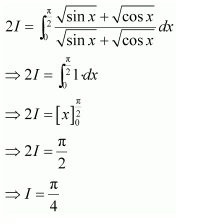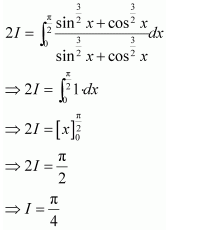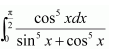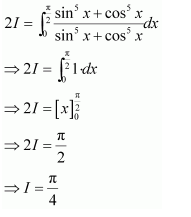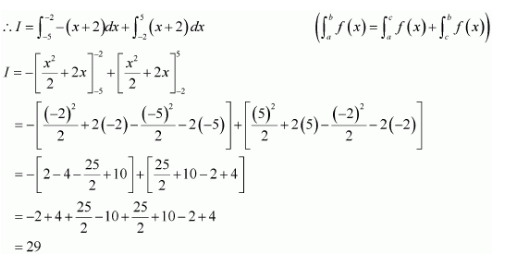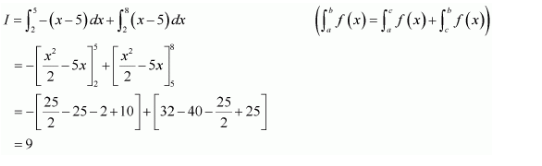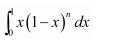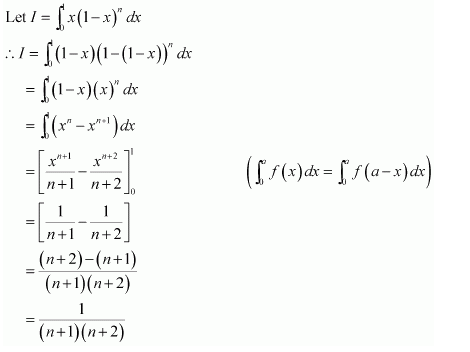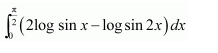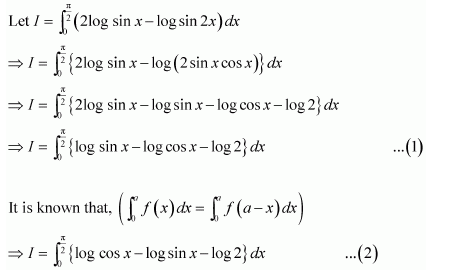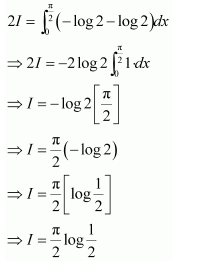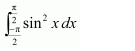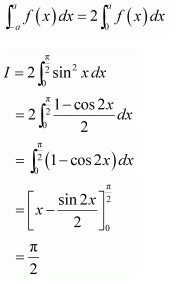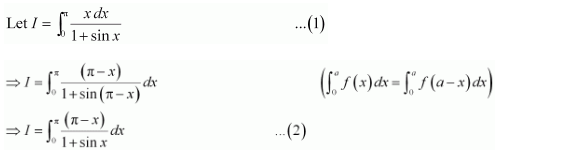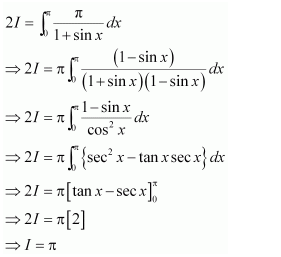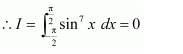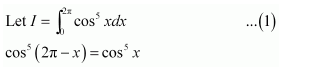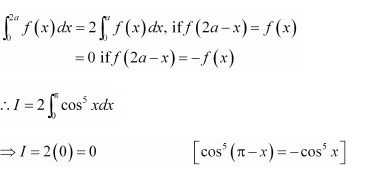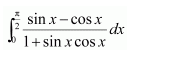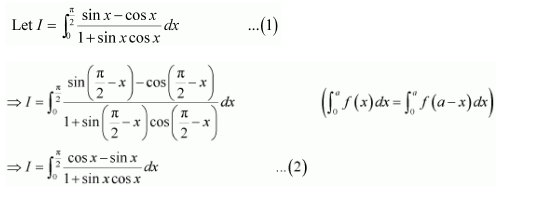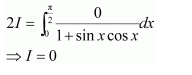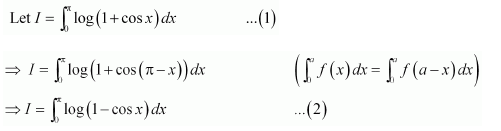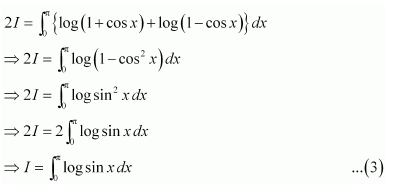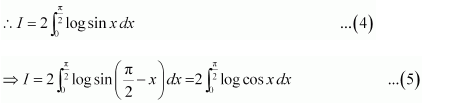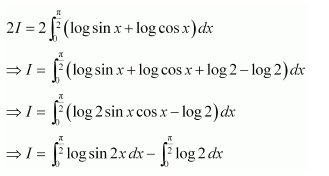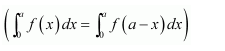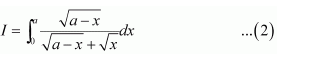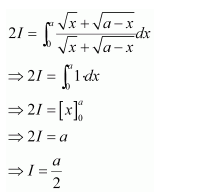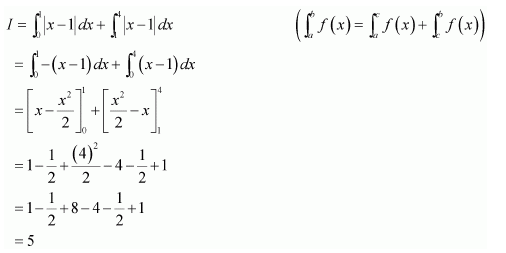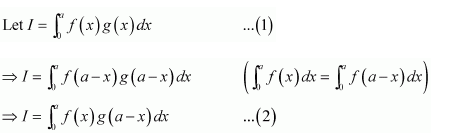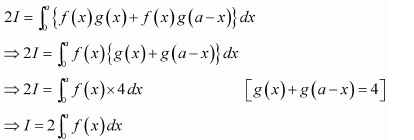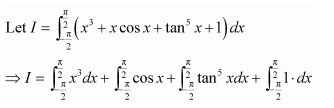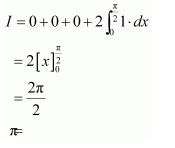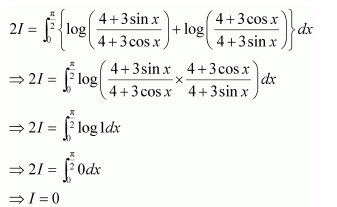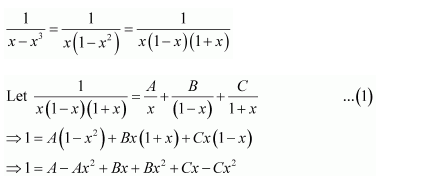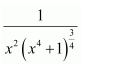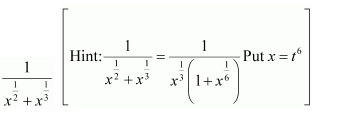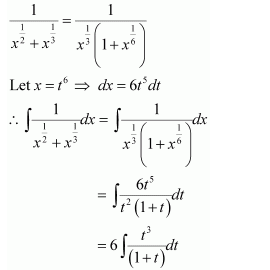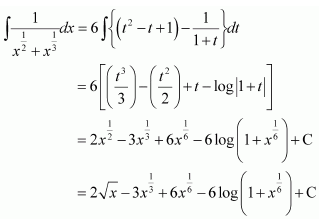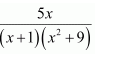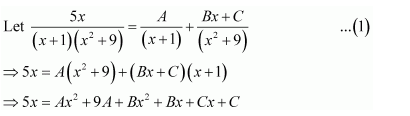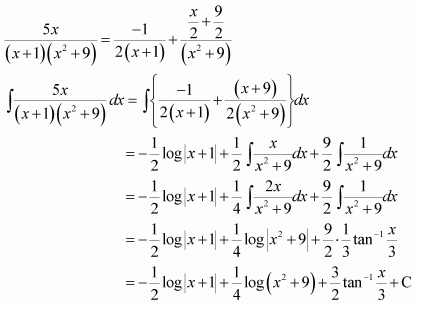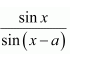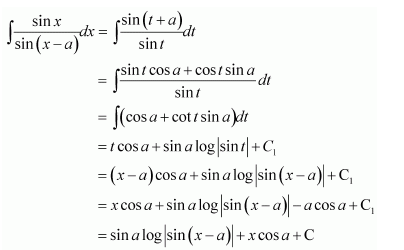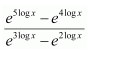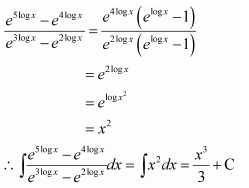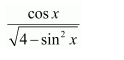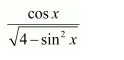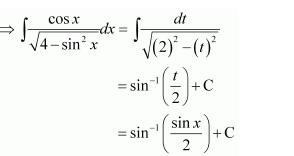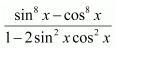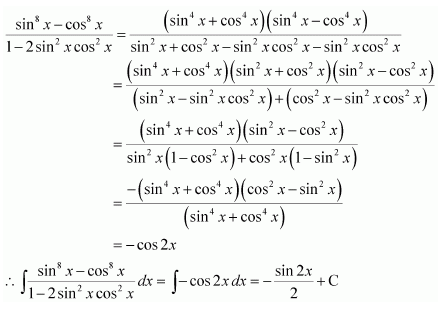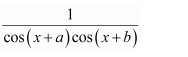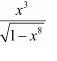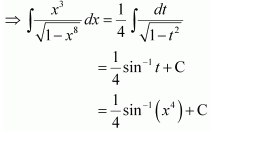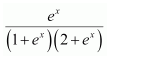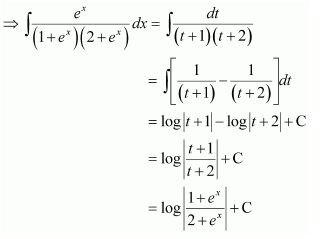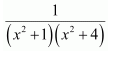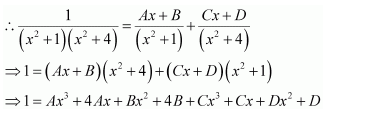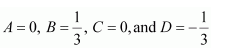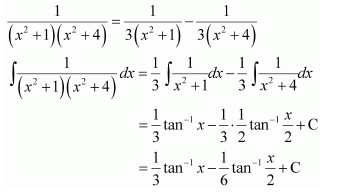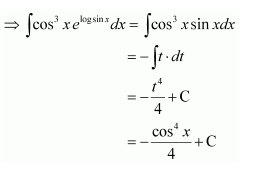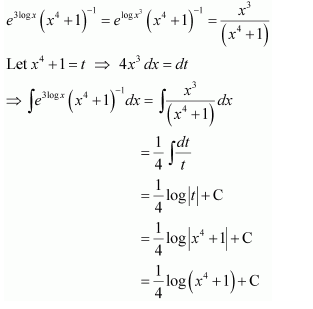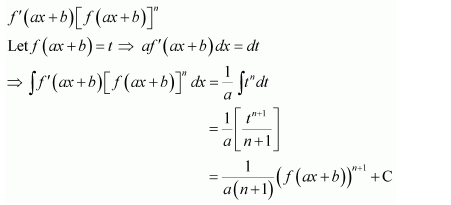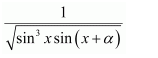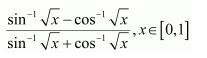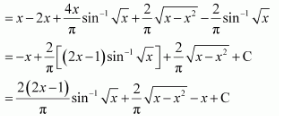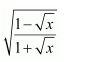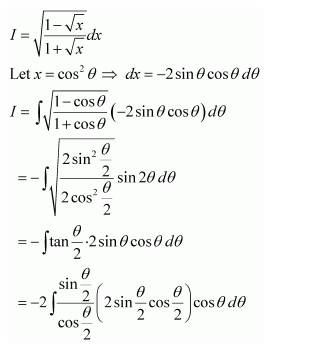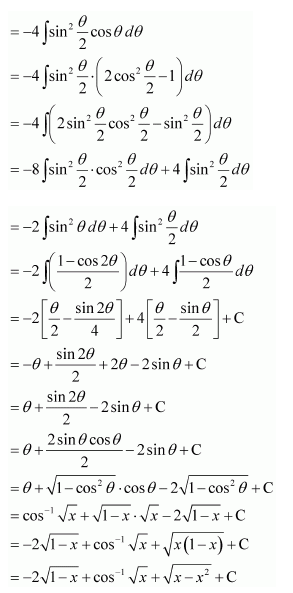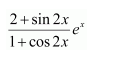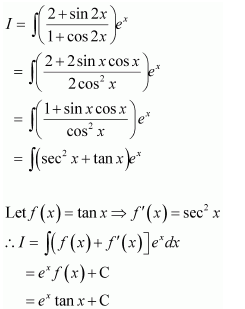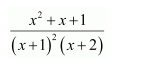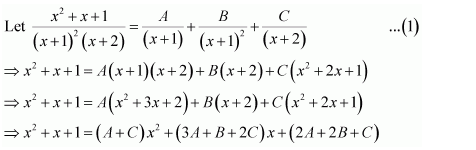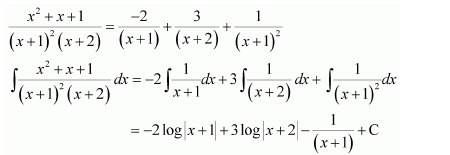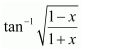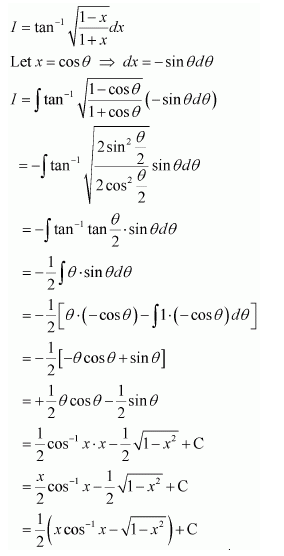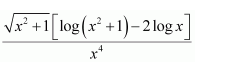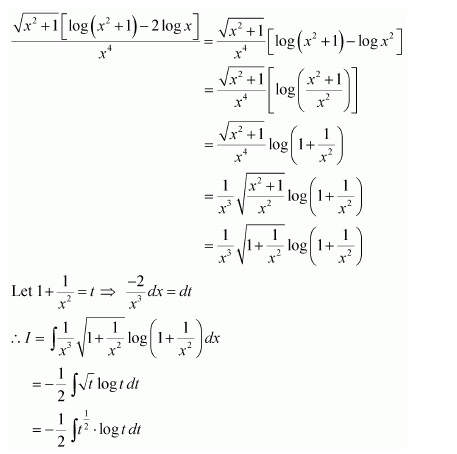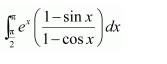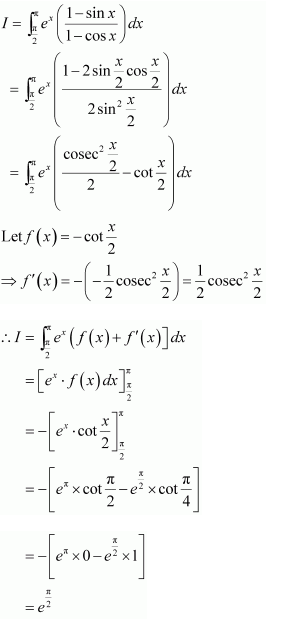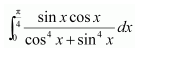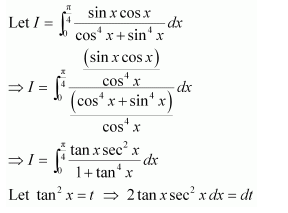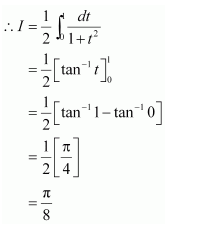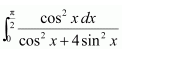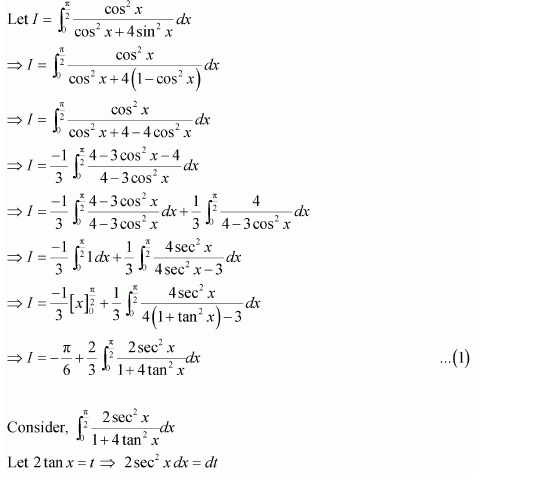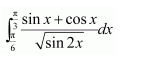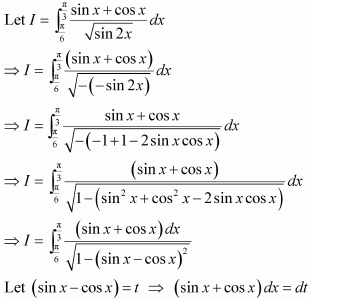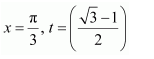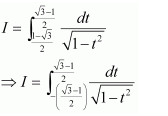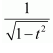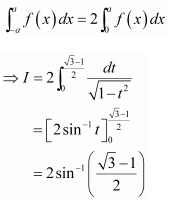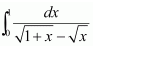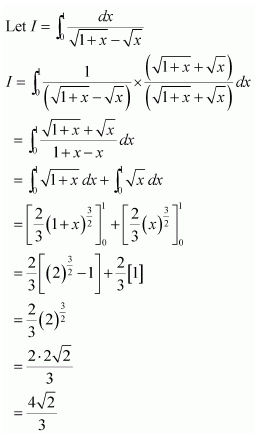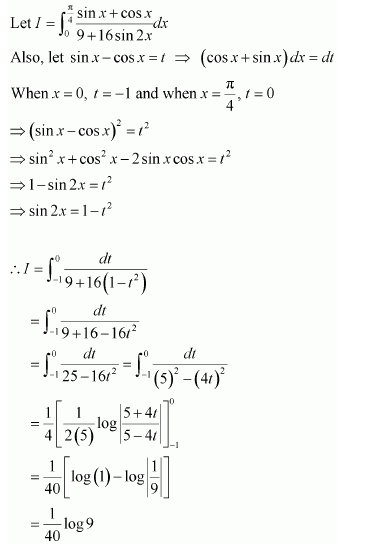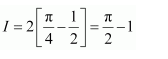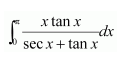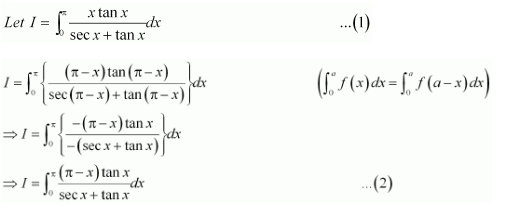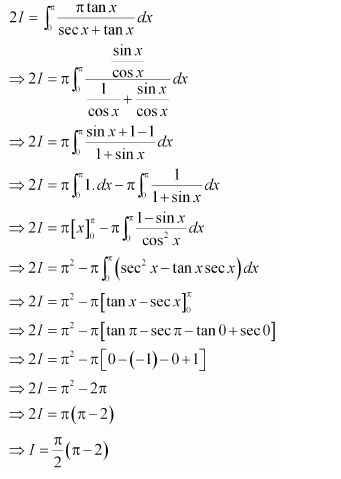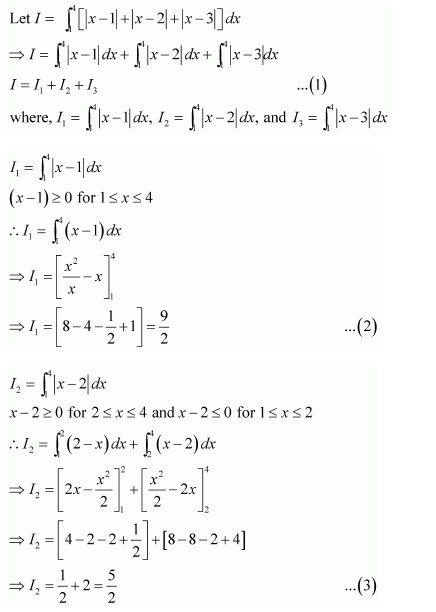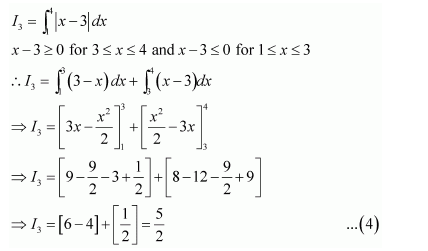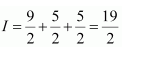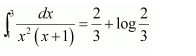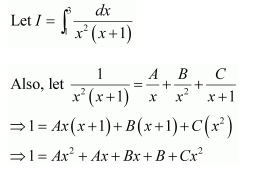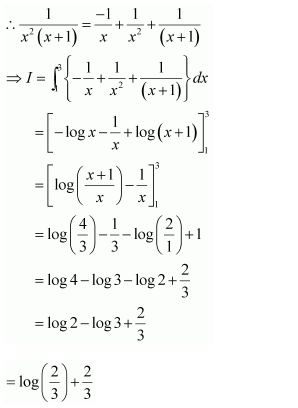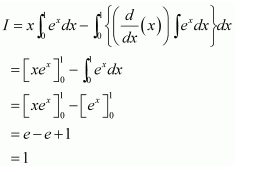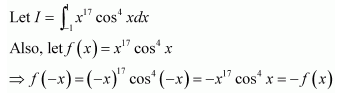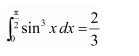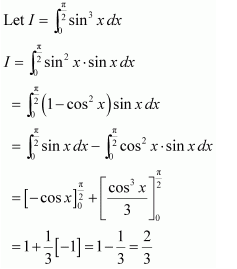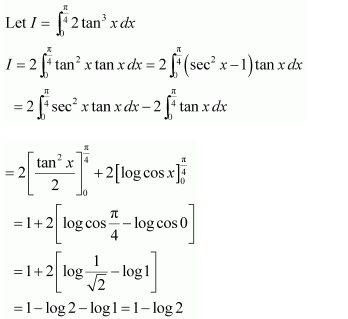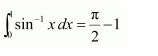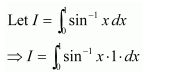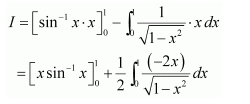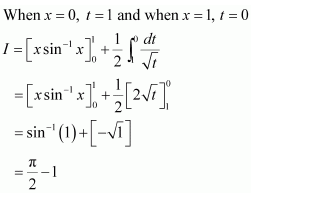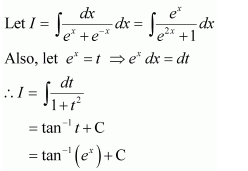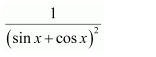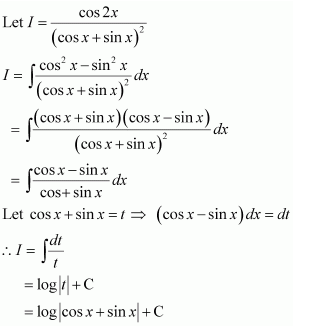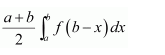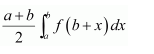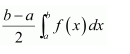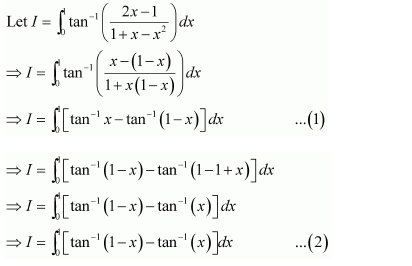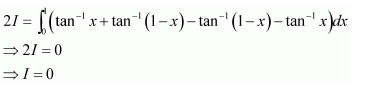NCERT Solutions For Class 12 Maths Chapter 7 clears all the doubts regarding the chapter on Integrals and Questions are solved in a simple way. Students who are appearing for CBSE Class 12 board exams can download Chapter 7 Integrals Class 12 NCERT Solutions. In this chapter, each question was solved by the best teachers in India. All answers are given with a complete explanation. This will helps to get a better score in the examination. Class 12 Maths NCERT Solutions Chapter 7 will give you the best results in the CBSE board exams. Maths is the most important and scoring subject in the board exams. There are 10 exercises in NCERT Solutions For Class 12 Maths Chapter 7. Experts are given detailed explanations for the students. NCERT Solutions For Class 12 is useful for the students who are going to attempt JEE Mains, JEE Advance. It will help to get the best score in the exam and you can complete your home assignments as well as revision purposes.
NCERT Solutions Class 12 Maths Chapter 7 Integrals
| Section no | Topic Name |
| 7.1 | Introduction |
| 7.2 | Integration as an Inverse Process of Differentiation |
| 7.3 | Methods of Integration |
| 7.4 | Integrals of Some Particular Functions |
| 7.5 | Integration by Partial Fractions |
| 7.6 | Integration by Parts |
| 7.7 | Definite Integral |
| 7.8 | Fundamental Theorem of Calculus |
| 7.9 | Evaluation of Definite Integrals by Substitution |
| 7.10 | Some Properties of Definite Integrals |
NCERT Solutions For Class 12 Maths Chapter 7 Ex 7.1 Introduction
Question 1:
Sin 2x
Answer:
The antiderivative of sin 2x is a function of x whose derivative is sin 2x.
It is known that,
Therefore, the antiderivative of sin 2x is
Question 2:
Cos 3x
Answer:
The antiderivative of cos 3x is a function of x whose derivative is cos 3x
It is known that,
Therefore, the antiderivative of cos 3x is
Question 3:
e2x
Answer:
The antiderivative of e2x is the function of x whose derivative is e2x.
It is known that,
Therefore, the antiderivative of
Question 4:
Answer:
The antiderivative of
is the function of x whose derivative is
It is known that,
Therefore, the antiderivative of is
Question 5:
Answer:
The antiderivative of is the function of x whose derivative is
It is known that,
Therefore, the antiderivative of is
Question 6:
Answer:
Question 7:
Answer:
Question 8:
Answer:
Question 9:
Answer:
Question 10:
Answer:
Question 11:
Answer:
Question 12:
Answer:
Question 13:
Answer:
On dividing, we obtain
Question 14:
Answer:
Question 15:
Answer:
Question 16:
Answer:
Question 17:
Answer:
Question 18:
Answer:
Question 19:
Answer:
Question 20:
Answer:
Question 21:
The antiderivative of 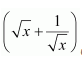
(A)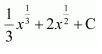
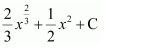
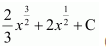
Answer:
Hence, the correct answer is C.
Question 22:
If 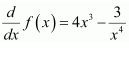
(A)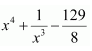
(C)
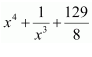
Answer:
It is given that
∴Antiderivative of
also
f(2)=0
Hence, the correct answer is A.
NCERT Solutions For Class 12 Maths Chapter 7 Integrals Ex 7.2 Integration as an Inverse Process of Differentiation
Question 1:
Answer:
Let =t
∴2x dx = dt
Question 2:
Answer:
Let log |x| = t
Question 3:
Answer:
Let 1 + log x = t
∴
Question 4:
Sin x.Sin (Cos x)
Answer:
in x ⋅ sin (cos x)
Let cos x = t
∴ −sin x dx = dt
Question 5:
sin(ax+b)cos(ax+b)
Answer:
let 2(ax+b)=t
∴ 2adx = dt
Question 6:
Answer:
Let ax + b = t
⇒ adx = dt
Question 7:
Answer:
let (x+2)=t
∴ dx = dt
Question 8:
Answer:
Let 1 + 2x2 = t
∴ 4xdx = dt
Question 9:
Answer:
Let
∴ (2x + 1)dx = dt
Question 10:
Answer:
let
∴
Question 11:
Answer:
Let x+4=t
⇒dx=dt,x=t-4
Question 12:
Answer:
Let
∴
Question 13:
Answer:
Let
∴ 9x2 dx = dt
Question 14:
Answer:
Let log x = t
∴
Question 15:
Answer:
Let
∴ −8x dx = dt
Question 16:
Answer:
Let 2x+3=t
∴ 2dx = dt
Question 17:
Answer:
Let
∴ 2xdx = dt
Question 18:
Answer:
Let
∴
Question 19:
Answer:
Dividing the numerator and denominator by ex, we obtain
Let
∴
Question 20:
Answer:
Let
∴
Question 21:
Answer:
Let 2x − 3 = t
∴ 2dx = dt
⇒∫tan22x-3dx = ∫sec22x-3 – 1dx=∫sec2t- 1dt2= 12∫sec2t dt – ∫1dt= 12tant – t + C= 12tan2x-3 – 2x-3 + C
Question 22:
Answer:
Let 7 − 4x = t
∴ −4dx = dt
Question 23:
Answer:
Let
∴
Question 24:
Answer:
Let 3 cos x+ 2 sin x =t
∴(-3 sin x +2 cos x)dx=dt
Question 25:
Answer:
Let (1-tan x)=t
∴
Question 26:
Answer:
Let
∴
Question 27:
Answer:
Let sin 2x = t
∴2 cos 2x dx=dt
Question 28:
Answer:
Let 1+sin x=t
∴ cos x dx = dt
Question 29:
cot x log sin x
Answer:
Let log sin x = t
Question 30:
Answer:
Let 1 + cos x = t
∴ −sin x dx = dt
Question 31:
Answer:
Let 1 + cos x = t
∴ −sin x dx = dt
Question 32:
Answer:
Let sin x + cos x = t ⇒ (cos x − sin x) dx = dt
Question 33:
Answer:
Put cos x − sin x = t ⇒ (−sin x − cos x) dx = dt
Question 34:
Answer:
Question 35:
Answer:
Let 1 + log x = t
∴
Question 36:
Answer:
Let (x+log x)=t
∴
Question 37:
Answer:
Let x4 = t
∴ 4x3 dx = dt
Let
∴
From (1), we obtain
Question 38:
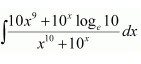
(A)(B)
(C)
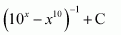
Answer:
Let
∴
Question 39:
equals
A. tan x +cot x+C
B. tan x-cot x+C
C.tan x cot x+C
D. tan x-cot 2x+C
Answer:
Hence, the correct answer is B.
NCERT Solutions For Class 12 Matas Chapter 7 Ex 7.3 Methods of Integration
Question 1:
Answer:
Question 2:
sin 3x cos 4x
Answer:
It is known that,
Question 3:
cos 2x cos 4x cos 6x
Answer:
It is known that,
Question 4:
Answer:
Let
Question 5:
Answer:
Question 6:
sin x sin 2x sin 3x
Answer:
It is known that,
Question 7:
sin 4x sin 8x
Answer:
It is known that,
sin A . sin B = 12cosA-B-cosA+B∴∫sin4x sin8x dx=∫12cos4x-8x-cos4x+8xdx=12∫cos-4x-cos12xdx=12∫cos4x-cos12xdx=12sin4x4-sin12x12+C
Question 8:
Answer:
Question 9:
Answer:
Question 10:
sin4x
Answer:
Question 11:
cos4 2x
Answer:
Question 12:
Answer:
Question 13:
Answer:
Question 14:
Answer:
Question 15:
Answer:
Question 16:
Answer:
From equation (1), we obtain
Question 17:
Answer:
Question 18:
Answer:
Question 19:
Answer:
1sinxcos3x=sin2x+cos2xsinxcos3x=sinxcos3x+1sinxcosx
⇒1sinxcos3x=tanxsec2x+1cos2xsinxcosxcos2x=tanxsec2x+sec2xtanx
Question 20:
Answer:
Question 21:
sin−1 (cos x)
Answer:
It is known that,
Substituting in equation (1), we obtain
Question 22:
Answer:
Question 23:
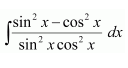
A. tan x + cot x + C
B. tan x + cosec x + C
C. − tan x + cot x + C
D. tan x + sec x + C
Answer:
Hence, the correct answer is A.
Question 24:
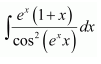
A. − cot (exx) + C
B. tan (xex) + C
C. tan (ex) + C
D. cot (ex) + C
Answer:
Let exx = t
NCERT Solutions For Class 12 Matas Chapter 7 Ex 7.4 Integrals of Some Particular Functions
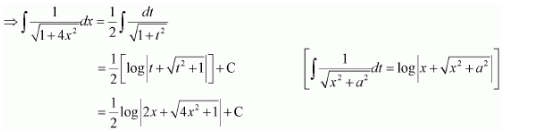
Question 1:
Answer:
Let x3 = t
∴ 3x2 dx = dt
Question 2:
Answer:
Let 2x = t
∴ 2dx = dt
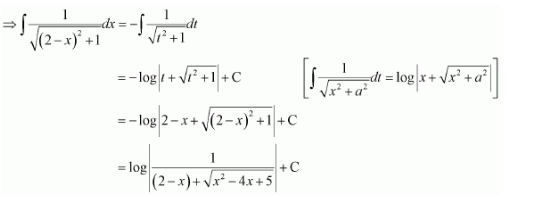
Question 3:
Answer:
Let 2 − x = t
⇒ −dx = dt
Question 4:
Answer:
Let 5x = t
∴ 5dx = dt
Question 5:
Answer:
Question 6:
Answer:
Let x3 = t
∴ 3x2 dx = dt
Question 7:
Answer:
From (1), we obtain
Question 8:
Answer:
Let x3 = t
⇒ 3x2 dx = dt
Question 9:
Answer:
Let tan x = t
∴ sec2x dx = dt
Question 10:
Answer:
Question 11:
19×2+6x+5
Answer:
∫19×2+6x+5dx=∫13x+12+22dx
Let (3x+1)=t
∴3 dx=dt
⇒∫13x+12+22dx=13∫1t2+22dt
=13×2tan-1t2+C
=16tan-13x+12+C
Question 12:
Answer:
Question 13:
Answer:
Question 14:
Answer:
Question 15:
Answer:
Question 16:
Answer:
Equating the coefficients of x and constant term on both sides, we obtain
4A = 4 ⇒ A = 1
A + B = 1 ⇒ B = 0
Let 2x2 + x − 3 = t
∴ (4x + 1) dx = dt
Question 17:
Answer:
Equating the coefficients of x and constant term on both sides, we obtain
From (1), we obtain
From equation (2), we obtain
Question 18:
Answer:
Equating the coefficient of x and constant term on both sides, we obtain
therefore
Substituting equations (2) and (3) in equation (1), we obtain
Question 19:
Answer:
Equating the coefficients of x and constant term, we obtain
2A = 6 ⇒ A = 3
−9A + B = 7 ⇒ B = 34
∴ 6x + 7 = 3 (2x − 9) + 34
Substituting equations (2) and (3) in (1), we obtain
Question 20:
Answer:
Equating the coefficients of x and constant term on both sides, we obtain
Using equations (2) and (3) in (1), we obtain
Question 21:
Answer:
Let x2 + 2x +3 = t
⇒ (2x + 2) dx =dt
Using equations (2) and (3) in (1), we obtain
Question 22:
Answer:
Equating the coefficients of x and constant term on both sides, we obtain
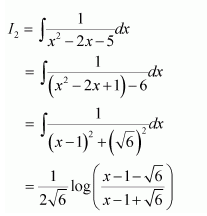
Substituting (2) and (3) in (1), we obtain
Question 23:
Answer:
Equating the coefficients of x and constant term, we obtain
Using equations (2) and (3) in (1), we obtain
Question 24:
equals
A. x tan−1 (x + 1) + C
B. tan− 1 (x + 1) + C
C. (x + 1) tan−1 x + C
D. tan−1 x + C
Answer:
Hence, the correct answer is B.
Question 25:
A.
B.
C.
D.
Answer:
Hence, the correct answer is B.
NCERT Solutions Class 12 Maths Chapter 7 Integrals Ex 7.5 Integration by Partial Fractions
Question 1:
Answer:
Let
⇒x=A(x+2)+B(x+1)
Equating the coefficients of x and constant term, we obtain
A + B = 1
2A + B = 0
On solving, we obtain
A = −1 and B = 2
Question 2:
Answer:
Let
1=A(x-3)+B(x+3)
Equating the coefficients of x and constant term, we obtain
A + B = 0
−3A + 3B = 1
On solving, we obtain
Question 3:
Answer:
Let
3x-1=A(x-2)(x-3)+B(x-1)(x-3)+C(x-1)(x-2)……..(1)
Substituting x = 1, 2, and 3 respectively in equation (1), we obtain A = 1, B = −5, and C = 4
Question 4:
Answer:
Let
x=A(x-2)(x-3)+B(x-1)(x-3)+C(x-1)(x-2)………(1)
Substituting x = 1, 2, and 3 respectively in equation (1), we obtain
Question 5:
Answer:
Let
2x=A(x+2)+B(x+1)…….(1)
Substituting x = −1 and −2 in equation (1), we obtain
A = −2 and B = 4
Question 6:
Answer:
It can be seen that the given integrand is not a proper fraction.
Therefore, on dividing (1 − x2) by x(1 − 2x), we obtain
Substituting x = 0 and
in equation (1), we obtain
A = 2 and B = 3
Substituting equation (1), we obtain
Question 7:
Answer:
Let
Equating the coefficients of x2, x, and constant term, we obtain
A + C = 0
−A + B = 1
−B + C = 0
On solving these equations, we obtain
From equation (1), we obtain
Question 8:
Answer:
Let
Substituting x = 1, we obtain
Equating the coefficients of x2 and constant term, we obtain
A + C = 0
−2A + 2B + C = 0
On solving, we obtain
Question 9:
Answer:
Let
Substituting x = 1 in equation (1), we obtain
B = 4
Equating the coefficients of x2 and x, we obtain
A + C = 0
B − 2C = 3
On solving, we obtain
Question 10:
Answer:
Let
Question 11:
Answer:
Let
Substituting x = −1, −2, and 2 respectively in equation (1), we obtain
Question 12:
Answer:
It can be seen that the given integrand is not a proper fraction.
Therefore, on dividing (x3 + x + 1) by x2 − 1, we obtain
Let
2x+1=A(x-1)+B(x+1)……..(1)
Substituting x = 1 and −1 in equation (1), we obtain
Question 13:
Answer:
Equating the coefficient of x2, x, and constant term, we obtain
A − B = 0
B − C = 0
A + C = 2
On solving these equations, we obtain
A = 1, B = 1, and C = 1
Question 14:
Answer:
Equating the coefficient of x and constant term, we obtain
A = 3
2A + B = −1 ⇒ B = −7
Question 15:
Answer:
Equating the coefficient of x3, x2, x, and constant term, we obtain
By solving these equations, we obtain
Question 16:
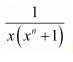
Multiplying the numerator and denominator by xn − 1, we obtain
Substituting t = 0, −1 in equation (1), we obtain
A = 1 and B = −1
Question 17:
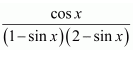
Substituting t = 2 and then t = 1 in equation (1), we obtain
A = 1 and B = −1
Question 18:
Answer:
Equating the coefficients of x3, x2, x, and constant term, we obtain
A + C = 0
B + D = 4
4A + 3C = 0
4B + 3D = 10
On solving these equations, we obtain
A = 0, B = −2, C = 0, and D = 6
Question 19:
Answer:
Let x2 = t ⇒ 2xdx = dt
Substituting t = −3 and t = −1 in equation (1), we obtain
Question 20:
Answer:
Multiplying the numerator and denominator by x3, we obtain
Let x4 = t ⇒ 4x3dx = dt
Substituting t = 0 and 1 in (1), we obtain
A = −1 and B = 1
Question 21:
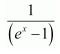
Let ex = t ⇒ exdx = dt
Substituting t = 1 and t = 0 in equation (1), we obtain
A = −1 and B = 1
Question 22:
A.
B.
C.
D.
Answer:
Substituting x = 1 and 2 in (1), we obtain
A = −1 and B = 2
Hence, the correct answer is B.
Question 23:
A.
B.
C.
D.
Answer:
Equating the coefficients of x2, x, and constant term, we obtain
A + B = 0
C = 0
A = 1
On solving these equations, we obtain
A = 1, B = −1, and C = 0
Hence, the correct answer is A.
NCERT Solutions Class 12 Maths Chapter 7 Integrals Ex 7.6 Integration by Parts
Question 1:
x sin x
Answer:
Let l=
Taking x as first function and sin x as second function and integrating by parts, we obtain
Question 2:
x sin 3x
Answer:
Let l=
Taking x as first function and sin 3x as second function and integrating by parts, we obtain
Question 3:
Answer:
Let
Taking x2 as first function and ex as second function and integrating by parts, we obtain
Again integrating by parts, we obtain
Question 4:
x log x
Answer:
let
Taking log x as first function and x as second function and integrating by parts, we obtain
Question 5:
x log 2x
Answer:
Let
Taking log 2x as first function and x as second function and integrating by parts, we obtain
Question 6:
x2log x
Answer:
Let
Taking log x as first function and x2 as second function and integrating by parts, we obtain
Question 7:
Answer:
Let
Taking as first function and x as second function and integrating by parts, we obtain
Question 8:
Answer:
Let
Taking as first function and x as second function and integrating by parts, we obtain
Question 9:
Answer:
Let
Taking cos−1 x as first function and x as second function and integrating by parts, we obtain
Question 10:
Answer:
Let
Taking as first function and 1 as second function and integrating by parts, we obtain
Question 11:
Answer:
Let
Taking as first function and
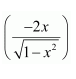
Question 12:
Answer:
Let
Taking x as first function and sec2x as second function and integrating by parts, we obtain
Question 13:
Answer:
Let
Taking as first function and 1 as second function and integrating by parts, we obtain
Question 14:
Answer:
Taking
as first function and x as second function and integrating by parts, we obtain
I=log x 2∫xdx-∫ddxlog x 2∫xdxdx=x22log x 2-∫2log x .1x.x22dx=x22log x 2-∫xlog x dx
Again integrating by parts, we obtain
I = x22logx 2-log x ∫x dx-∫ddxlog x ∫x dxdx=x22logx 2-x22log x -∫1x.x22dx=x22logx 2-x22log x +12∫x dx=x22logx 2-x22log x +x24+C
Question 15:
Answer:
let
Let I = I1 + I2 … (1)
Where, and
Taking log x as first function and x2 as second function and integrating by parts, we obtain
Taking log x as first function and 1 as second function and integrating by parts, we obtain
Using equations (2) and (3) in (1), we obtain
Question 16:
Answer:
Let
Let f(x)=sin x
⇒f’(x)=cos x
∴
It is known that,
∴
Question 17:
Answer:
Let
Let
It is known that,
Question 18:
Answer:
Let
It is known that,
From equation (1), we obtain
Question 19:
Answer:
Also, let
It is known that,
Question 20:
Answer:
Let
It is known that,
Question 21:
Answer:
Let
Integrating by parts, we obtain
Again integrating by parts, we obtain
Question 22:
Answer:
Let
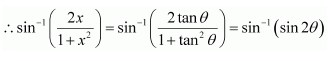
⇒
Integrating by parts, we obtain
Question 23:
equals
(A)(B)
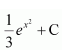
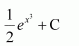
Answer:
Let
Also, let
Hence, the correct answer is A.
Question 24:
equals
(A) (B)
(C)
(D)
Answer:
Let
Also, let
It is known that,
Hence, the correct answer is B.
NCERT Solutions For Class 12 Maths Chapter 7 Integrals Ex 7.7 Definite Integral
Question 1:
Answer:
Question 2:
Answer:
Question 3:
Answer:
Question 4:
Answer:
Question 5:
Answer:
Question 6:
Answer:
Question 7:
Answer:
Question 8:
Answer:
Question 9:
Answer:
Question 10:
is equal to
A.
B.
C.
D.
Answer:
Hence, the correct answer is A.
Question 11:
is equal to
A.
B.
C.
D.
Answer:
Hence, the correct answer is D.
NCERT Solutions For Class 12 Maths Chapter 7 Integrals Ex 7.8 Fundamental Theorem of Calculus
Question 1:
Answer:
It is known that,
Question 2:
Answer:
Let I=
It is known that,
Question 3:
Answer:
It is known that,
Question 4:
Answer:
It is known that,
From equations (2) and (3), we obtain
Question 5:
Answer:
Let I= ……….(1)
It is known that,
Question 6:
Answer:
It is known that,
NCERT Solutions For Class 12 Maths Chapter 7 Integrals EX 7.9 Evaluation of Definite Integrals by Substitution
Question 1:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 2:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 3:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 4:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 5:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 6:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 7:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 8:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 9:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 10:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 11:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 12:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 13:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 14:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 15:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 16:
Answer:
Let
Equating the coefficients of x and constant term, we obtain
A = 10 and B = −25
Substituting the value of I1 in (1), we obtain
Question 17:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 18:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 19:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 20:
Answer:
By the second fundamental theorem of calculus, we obtain
Question 21:
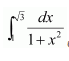
Answer:
A.
B.
C.
D.
Answer:
By the second fundamental theorem of calculus, we obtain
Hence, the correct answer is D.
Question 22:
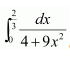
Answer:
A.
B.
C.
D.
Answer:
By the second fundamental theorem of calculus, we obtain
Hence, the correct answer is C.
NCERT Solutions For Class 12 Maths Chapter 7 Integrals Ex 7.10 Some Properties of Definite Integrals
Question 1:
Answer:
When x = 0, t = 1 and when x = 1, t = 2
Question 2:
Answer:
Also, let
Question 3:
Answer:
Let I=
Also, let x = tanθ ⇒ dx = sec2θ dθ
When x = 0, θ = 0 and when x = 1, θ=
Takingθas the first function and sec2θ as the second function and integrating by parts, we obtain
Question 4:
Answer:
Let x + 2 = t2 ⇒ dx = 2tdt
When x = 0, and when x = 2, t = 2
Question 5:
Answer:
Let cos x = t ⇒ −sinx dx = dt
When x = 0, t = 1 and when
Question 6:
Answer:
Let 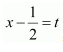
Question 7:
Answer:
Let x + 1 = t ⇒ dx = dt
When x = −1, t = 0 and when x = 1, t = 2
Question 8:
Answer:
Let 2x = t ⇒ 2dx = dt
When x = 1, t = 2 and when x = 2, t = 4
Question 9:
The value of the integral 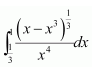
A. 6
B. 0
C. 3
D. 4
Answer:
Let cotθ = t ⇒ −cosec2θ dθ= dt
Hence, the correct answer is A.
Question 10:
If
A. cos x + x sin x
B. x sin x
C. x cos x
D. sin x + x cos x
Answer:
Integrating by parts, we obtain
Hence, the correct answer is B.
NCERT Solutions For Class 12 Maths Chapter 7 Integrals Ex 7.11
Question 1:
Answer:
Adding (1) and (2), we obtain
Question 2:
Answer:
Adding (1) and (2), we obtain
Question 3:
Answer:
Adding (1) and (2), we obtain
Question 4:
Answer:
Adding (1) and (2), we obtain
Question 5:
Answer:
Let I=
It can be seen that (x + 2) ≤ 0 on [−5, −2] and (x + 2) ≥ 0 on [−2, 5].
Question 6:
Answer:
Let I=
It can be seen that (x − 5) ≤ 0 on [2, 5] and (x − 5) ≥ 0 on [5, 8].
Question 7:
Answer:
Question 8:
Answer:
Question 9:
Answer:
Question 10:
Answer:
Adding (1) and (2), we obtain
Question 11:
Answer:
Let I =
As sin2 (−x) = (sin (−x))2 = (−sin x)2 = sin2x, therefore, sin2x is an even function.
It is known that if f(x) is an even function, then
Question 12:
Answer:
Adding (1) and (2), we obtain
Question 13:
Answer:
Let I= 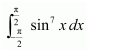
As sin7 (−x) = (sin (−x))7 = (−sin x)7 = −sin7x, therefore, sin2x is an odd function
It is known that, if f(x) is an odd function, then
Question 14:
Answer:
It is known that,
Question 15:
Answer:
Adding (1) and (2), we obtain
Question 16:
Answer:
Adding (1) and (2), we obtain
sin (π − x) = sin x
Adding (4) and (5), we obtain
Let 2x = t ⇒ 2dx = dt
When x = 0, t = 0 and when
x=π2, t=π∴
I=12∫0πlog sin tdt-π2log 2
⇒I=I2-π2log 2 [from 3]
⇒I2=-π2log 2
⇒I=-πlog 2
Question 17:
Answer:
Let I = 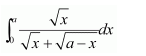
It is known that,
Adding (1) and (2), we obtain
Question 18:
Answer:
I =
It can be seen that, (x − 1) ≤ 0 when 0 ≤ x ≤ 1 and (x − 1) ≥ 0 when 1 ≤ x ≤ 4
Question 19:
Show that if f and g are defined as
and
Answer:
Adding (1) and (2), we obtain
Question 20:
The value of 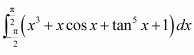
A. 0
B. 2
C. π
D. 1
Answer:
It is known that if f(x) is an even function, then
and if f(x) is an odd function, then
Hence, the correct answer is C.
Question 21:
The value of 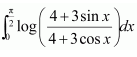
A. 2
B.
C. 0
D. -2
Answer:
Adding (1) and (2), we obtain
Hence, the correct answer is C.
NCERT Solutions For Class 12 Matas Chapter 7 Integrals Miscellaneous Solutions
Question 1:
Answer:
Equating the coefficients of x2, x, and constant term, we obtain
−A + B − C = 0
B + C = 0
A = 1
On solving these equations, we obtain
From equation (1), we obtain
Question 2:
Answer:
Question 3:
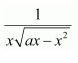
]
Answer:
Question 4:
Answer:
Question 5:
Answer:
On dividing, we obtain
Question 6:
Answer:
Equating the coefficients of x2, x, and constant term, we obtain
A + B = 0
B + C = 5
9A + C = 0
On solving these equations, we obtain
From equation (1), we obtain
Question 7:
Answer:
Let x − a = t ⇒ dx = dt
Question 8:
Answer:
Question 9:
Answer:
Let sin x = t ⇒ cos x dx = dt
Question 10:
Answer:
Question 11:
Answer:
Question 12:
Answer:
Let x4 = t ⇒ 4x3 dx = dt
Question 13:
Answer:
Let ex = t ⇒ ex dx = dt
Question 14:
Answer:
Equating the coefficients of x3, x2, x, and constant term, we obtain
A + C = 0
B + D = 0
4A + C = 0
4B + D = 1
On solving these equations, we obtain
From equation (1), we obtain
Question 15:
Answer:
= cos3 x × sin x
Let cos x = t ⇒ −sin x dx = dt
Question 16:
Answer:
Question 17:
Answer:
Question 18:
Answer:
Question 19:
Answer:
Let I=∫sin-1x-cos-1xsin-1x+cos-1xdx
It is known that, sin-1x+cos-1x=π2
⇒I=∫π2-cos-1x-cos-1xπ2dx
=2π∫π2-2cos-1xdx
=2π.π2∫1.dx-4π∫cos-1xdx
=x-4π∫cos-1xdx …(1)
Let I1=∫cos-1x dx
Also, let x=t⇒dx=2 t dt
⇒I1=2∫cos-1t.t dt
=2cos-1t.t22-∫-11-t2.t22dt
=t2cos-1t+∫t21-t2dt
=t2cos-1t-∫1-t2-11-t2dt
=t2cos-1t-∫1-t2dt+∫11-t2dt
=t2cos-1t-t21-t2-12sin-1t+sin-1t
=t2cos-1t-t21-t2+12sin-1t
From equation (1), we obtain
I=x-4πt2cos-1t-t21-t2+12sin-1t =x-4πxcos-1x-x21-x+12sin-1x
=x-4πxπ2-sin-1x-x-x22+12sin-1x
Question 20:
Answer:
Question 21:
Answer:
Question 22:
Answer:
Equating the coefficients of x2, x,and constant term, we obtain
A + C = 1
3A + B + 2C = 1
2A + 2B + C = 1
On solving these equations, we obtain
A = −2, B = 1, and C = 3
From equation (1), we obtain
Question 23:
Answer:
Question 24:
Answer:
Integrating by parts, we obtain
Question 25:
Answer:
Question 26:
Answer:
When x = 0, t = 0 and
Question 27:
Answer:
when x=0, t=0 and when
Question 28:
Answer:
when 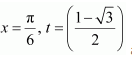
As 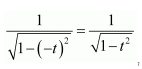
is an even function.
It is known that if f(x) is an even function, then
Question 29:
Answer:
Question 30:
Answer:
Question 31:
Answer:
From equation (1), we obtain
Question 32:
Answer:
Adding (1) and (2), we obtain
Question 33:
Answer:
From equations (1), (2), (3), and (4), we obtain
Question 34:
Answer:
Equating the coefficients of x2, x, and constant term, we obtain
A + C = 0
A + B = 0
B = 1
On solving these equations, we obtain
A = −1, C = 1, and B = 1
Hence, the given result is proved.
Question 35:
Answer:
Integrating by parts, we obtain
Hence, the given result is proved.
Question 36:
Answer:
Therefore, f (x) is an odd function.
It is known that if f(x) is an odd function, then
Hence, the given result is proved.
Question 37:
Answer:
Hence, the given result is proved.
Question 38:
Answer:
Hence, the given result is proved.
Question 39:
Answer:
Integrating by parts, we obtain
Let 1 − x2 = t ⇒ −2x dx = dt
Hence, the given result is proved.
Question 40:
Evaluate as a limit of a sum.
Answer:
Let I =
It is known that,
Question 41:
is equal to
A.
B.
C.
D.
Answer:
Hence, the correct answer is A.
Question 42:
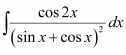
A.
B.
C.
D.
Answer:
Hence, the correct answer is B.
Question 43:
If f(a+b-x)=f(x), then is equal to
A.
B.
C.
D.
Answer:
Hence, the correct answer is D.
Question 44:
The value of 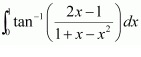
A. 1
B. 0
C. − 1
D.
Answer:
Adding (1) and (2), we obtain
Hence, the correct answer is B.