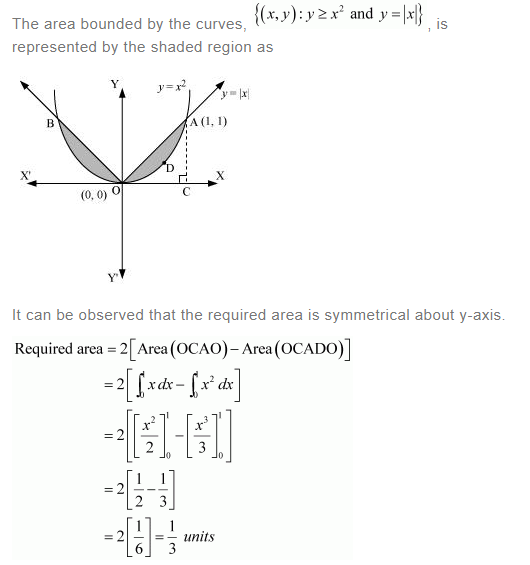
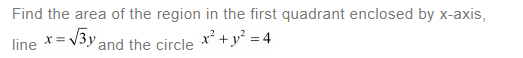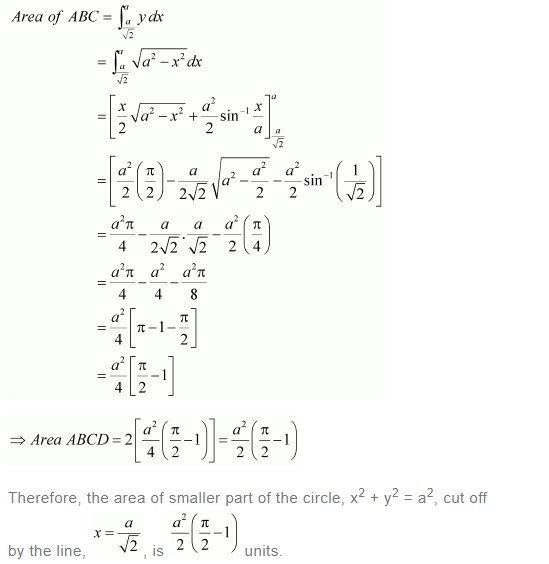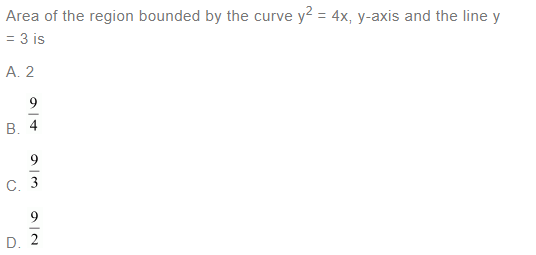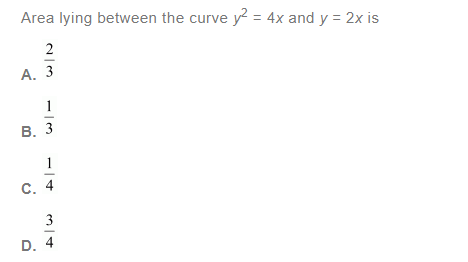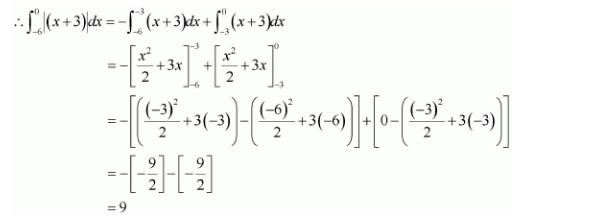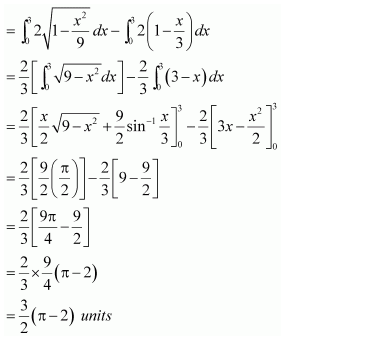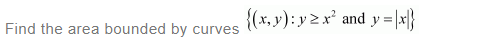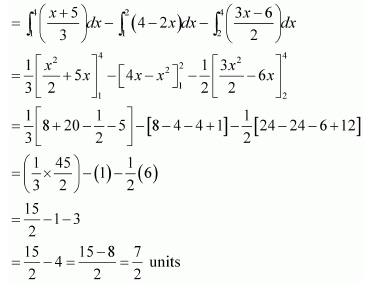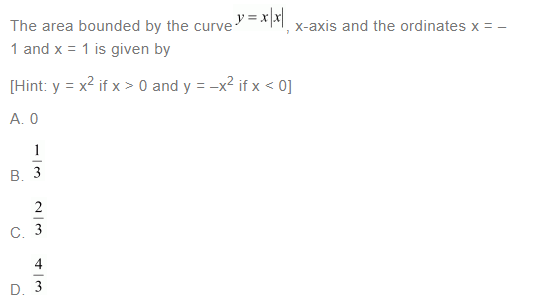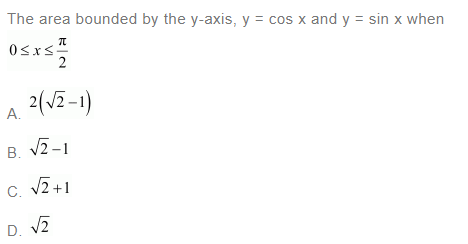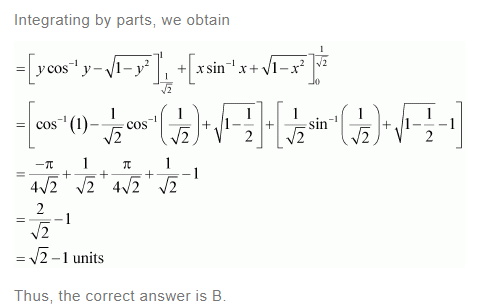NCERT Solutions For Class 12 Maths Chapter 8 is designed and prepared by India’s best teachers. This will helps you to clear all the doubts which are raised while in the preparation for the exams. Application Of Integrals Class 12 NCERT Solutions covers multiple exercises and each exercise is provided with a step-by-step explanation for better understanding. However, this chapter will be more useful and helpful for completing your home assignments as well as revision purposes. Class 12 Maths NCERT Solutions plays a prominent role in the preparation of exams. All important topics have been covered in this NCRET Solutions For Class 12 Maths Chapter 8. Professional Teachers give explanations in an easy manner. So you can get a better score in the examination. NCERT Solutions For Class 12 Maths will help the students for CBSE board exams and also for JEE Mains and Advance. Three exercises are given with diagrammatical explanations in the Application Of Integrals Class 12 NCERT Solutions.
NCERT Solutions For Class 12 Maths Chapter 8 Application Of Integrals
| Section No | Topic Name |
| 8 | Application Of Integrals |
| 8.1 | Introduction |
| 8.2 | Area Under Simple Curves |
| 8.3 | Area Between Two Curves |
NCERT Solutions For Class 12 Maths Chapter 8 Application Of Integrals Ex 8.1 Introduction
Question 1:
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Answer:
Question 2:
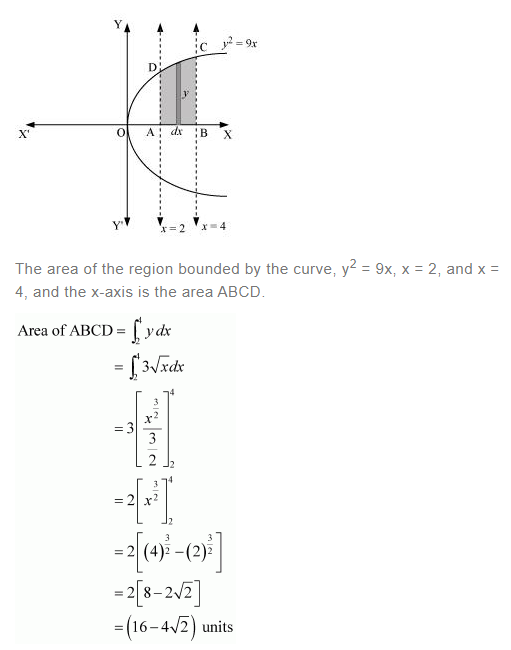
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Answer:
Question 3:
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Answer:
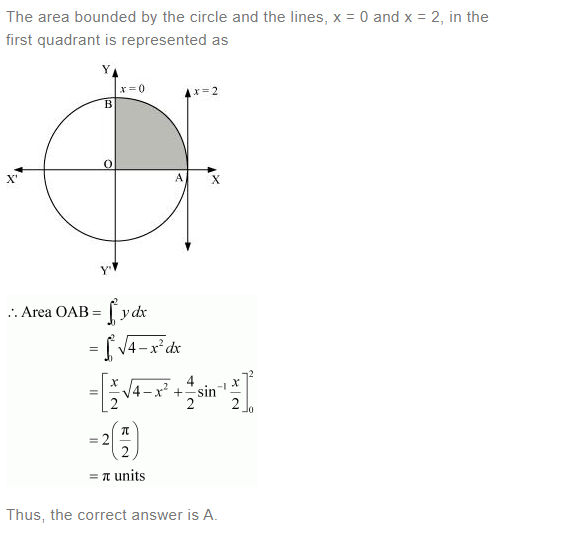
Question 4:
Answer:
Question 5:
Answer:
Question 6:
Answer:
Question 7:
Answer:
Question 8:
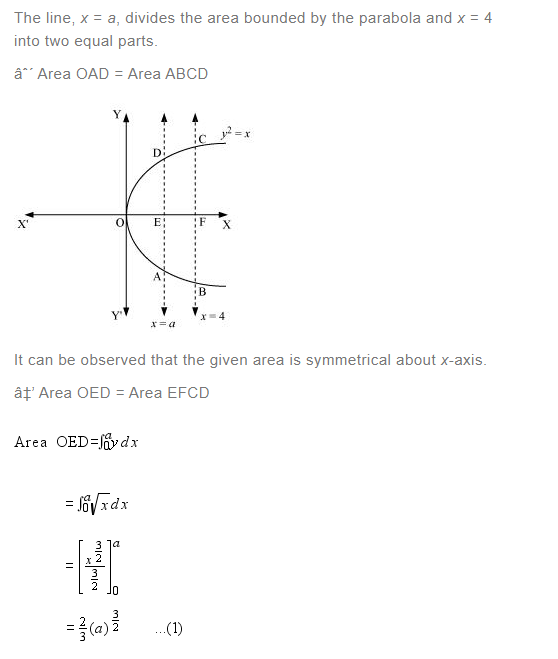
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Answer:
Question 9:
Answer:
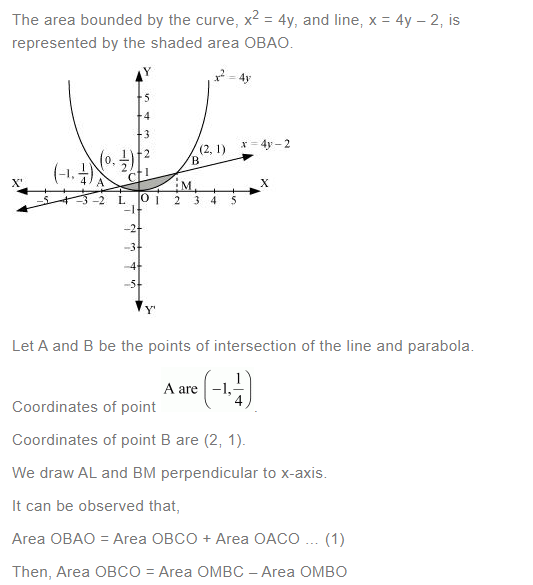
Question 10:
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Answer:
Question 11:
Find the area of the region bounded by the curve y2 = 4x and the line x = 3
Answer:
Question 12:
Answer:
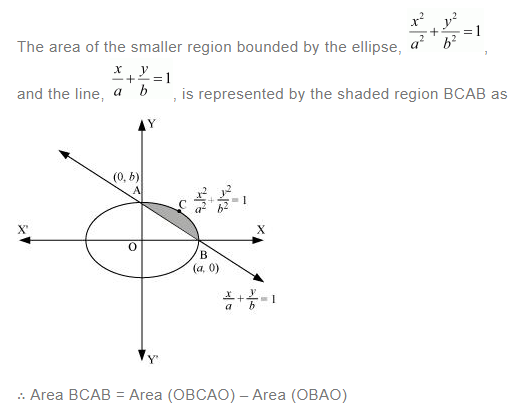
Question 13:
Answer:
NCERT Solutions For Class 12 Maths Chapter 8 Application Of Integrals Ex 8.2 Area Under Simple Curves
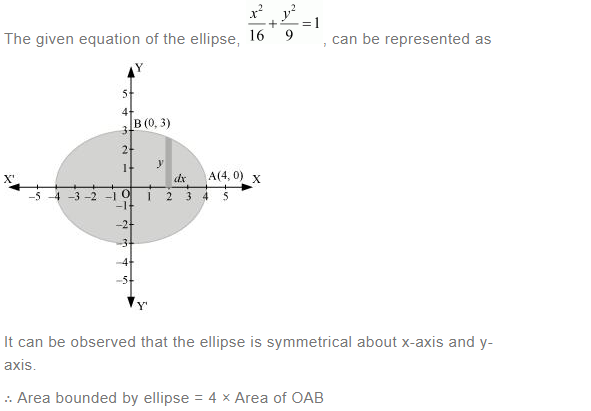
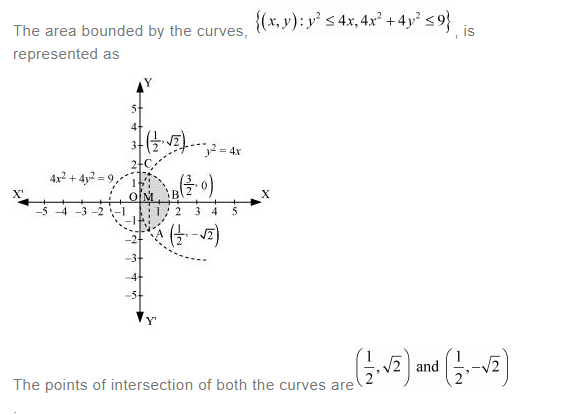
Question 1:
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
Answer:
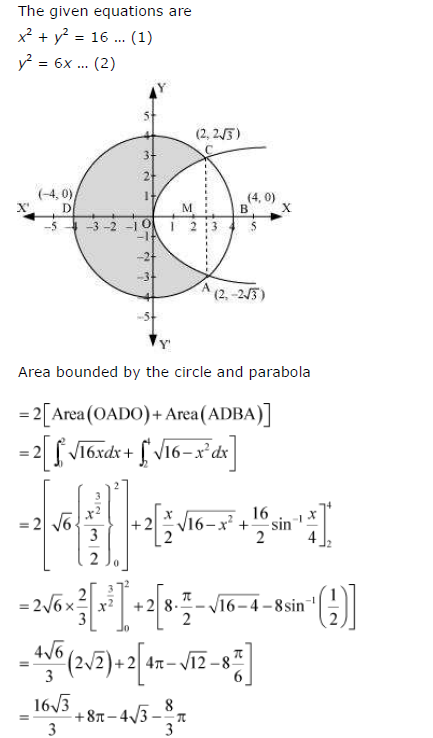
Question 2:
Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y 2 = 1
Answer:
Question 3:
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
Answer:
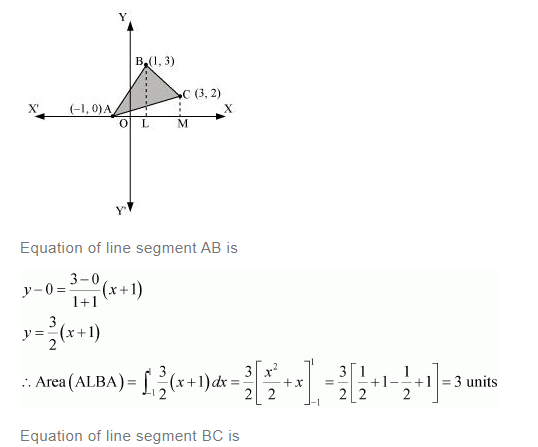
Question 4:
Using integration find the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3), and (3, 2).
Answer:
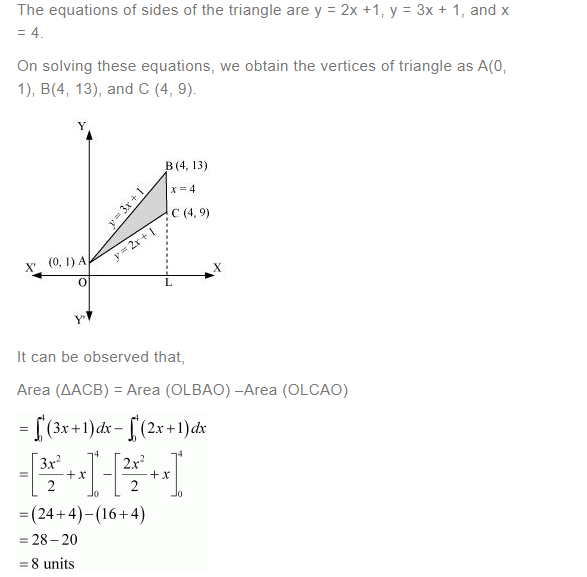
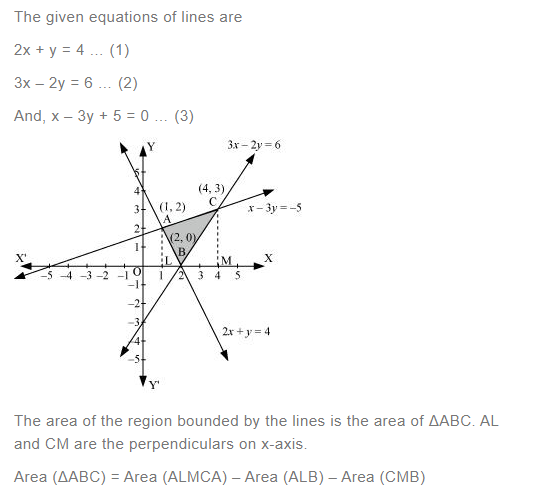
BL and CM are drawn perpendicular to x-axis.
It can be observed in the following figure that,
Area (ΔACB) = Area (ALBA) + Area (BLMCB) – Area (AMCA) … (1)
Question 5:
Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
Answer:
Question 6:
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
A. 2 (π – 2)
B. π – 2
C. 2π – 1
D. 2 (π + 2)
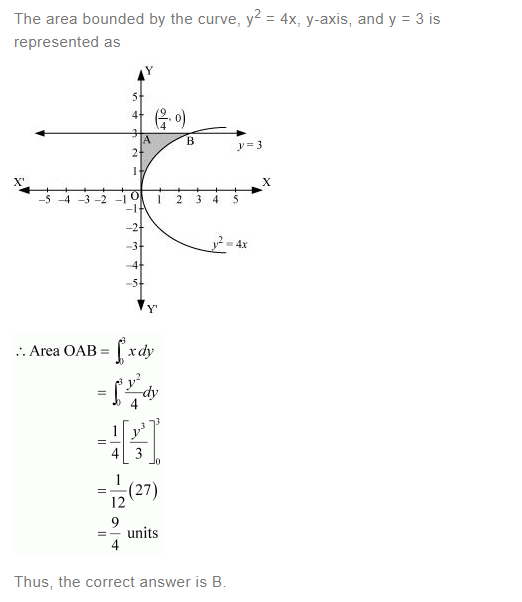
Answer:
Question 7:
Answer:
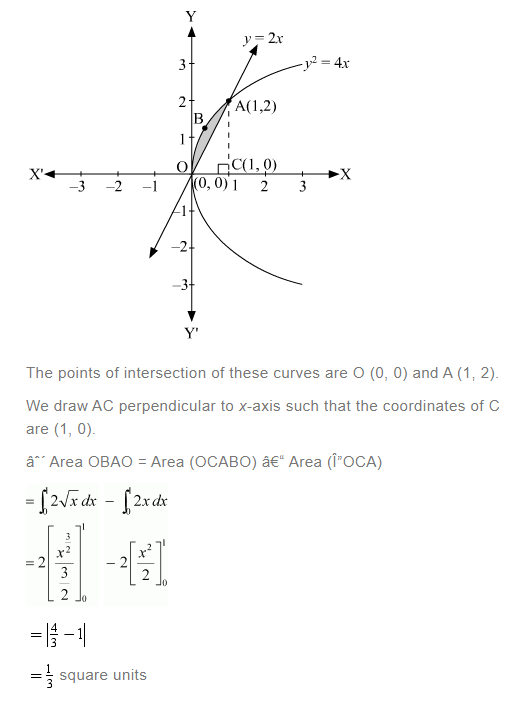
The area lying between the curve, y2 = 4x and y = 2x, is represented by the shaded area OBAO as
Thus, the correct answer is B.
NCERT Solutions For Class 12 Maths Chapter 8 Application Of Integrals Ex 8.3 Area Between Two Curves
Question 1:
Find the area under the given curves and given lines:
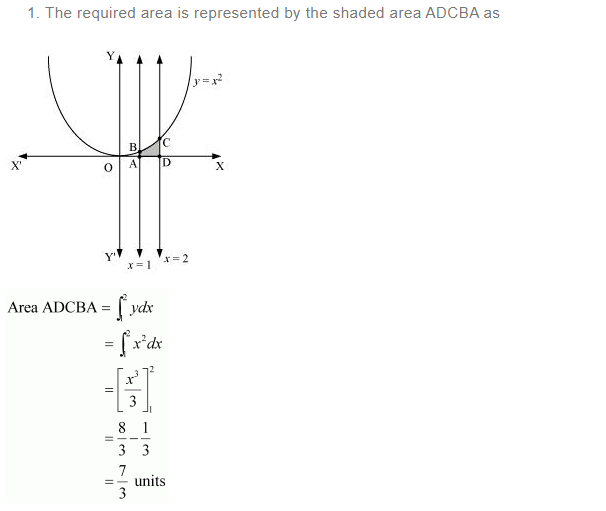
(i) y = x2, x = 1, x = 2 and x-axis
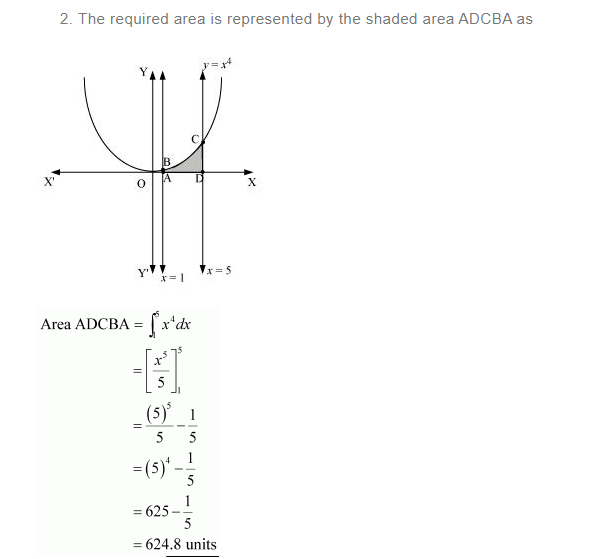
(ii) y = x4, x = 1, x = 5 and x –axis
Answer:
Question 2:
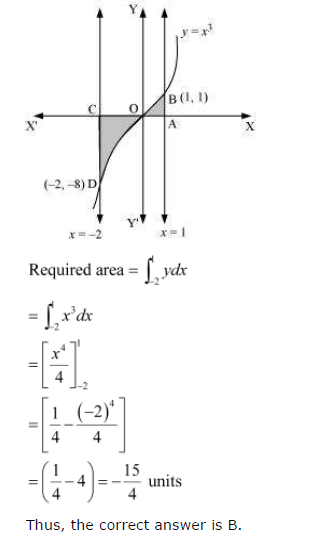
Find the area between the curves y = x and y = x2
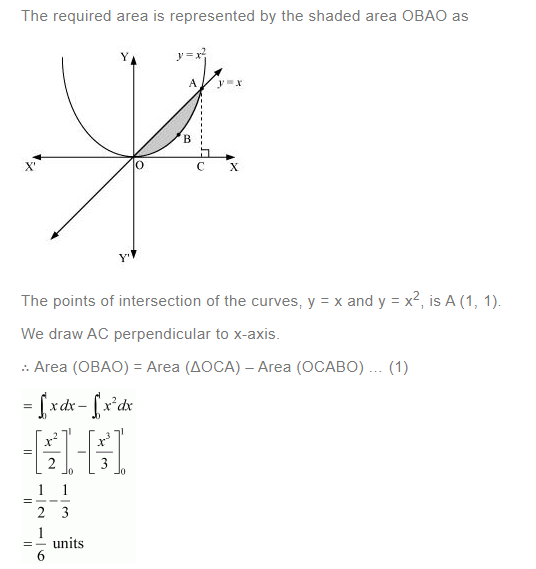
Question 3:
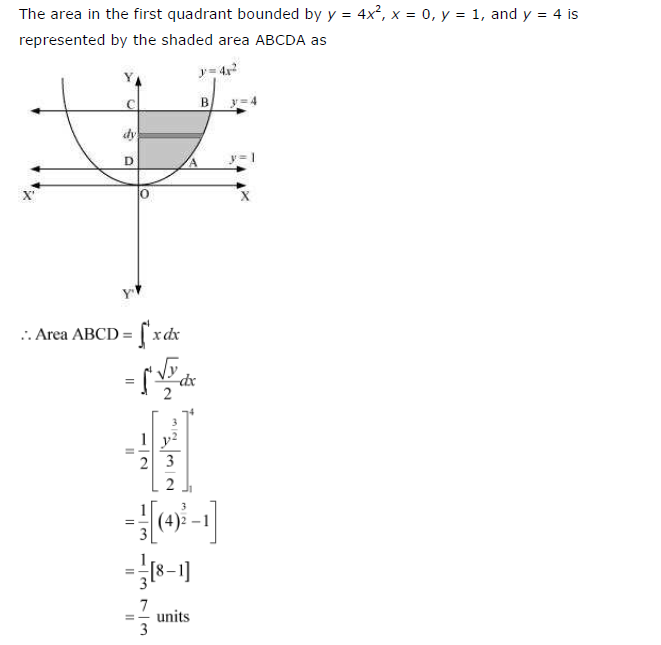
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1, and y = 4
Answer:
Question 4:
Answer:
Question 5:
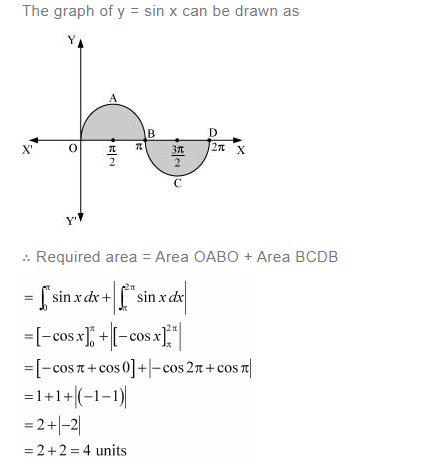
Find the area bounded by the curve y = sin x between x = 0 and x = 2π
Answer:
Question 6:
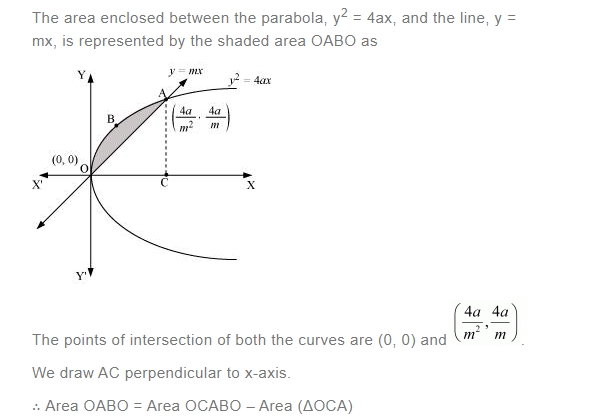
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Answer:
Question 7:
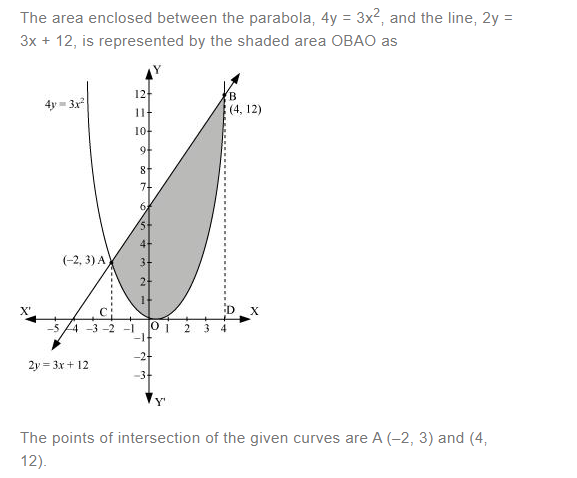
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Answer:
Question 8:
Answer:
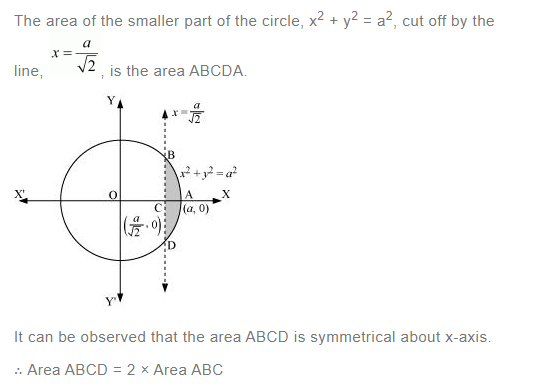
Question 9:
Answer:
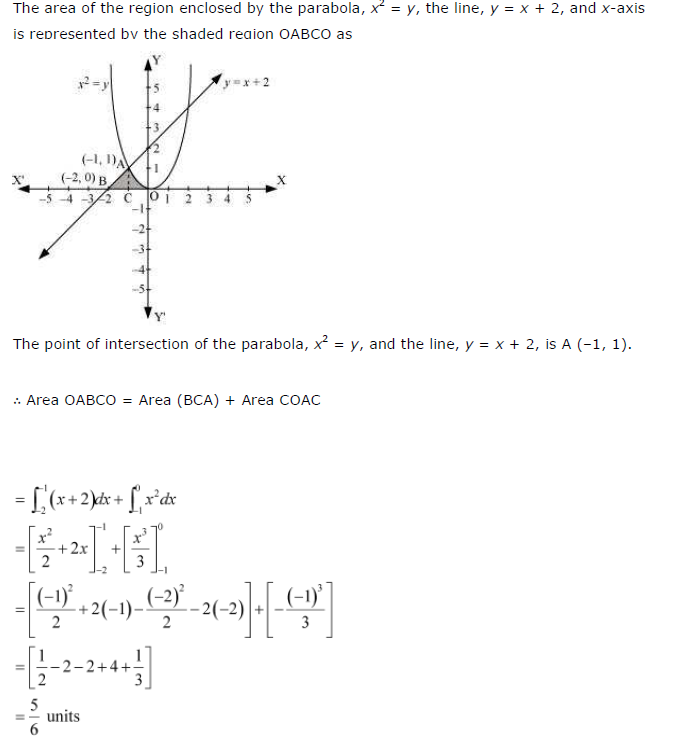
Question 10:
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis
Answer:
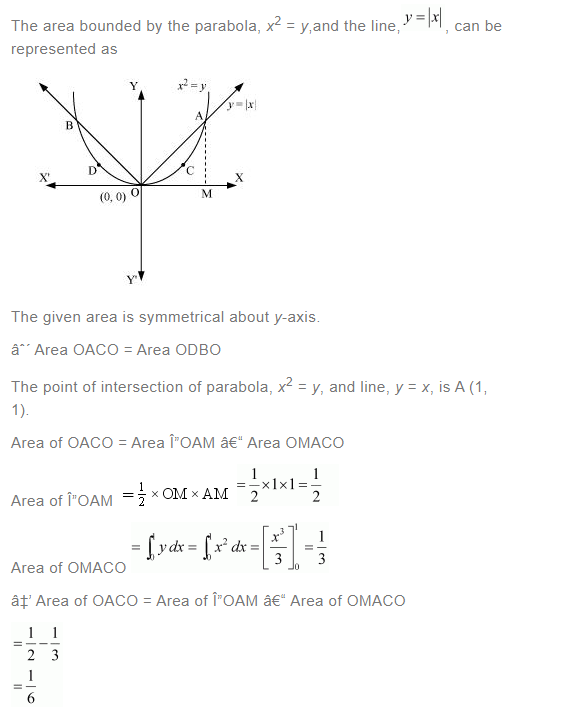
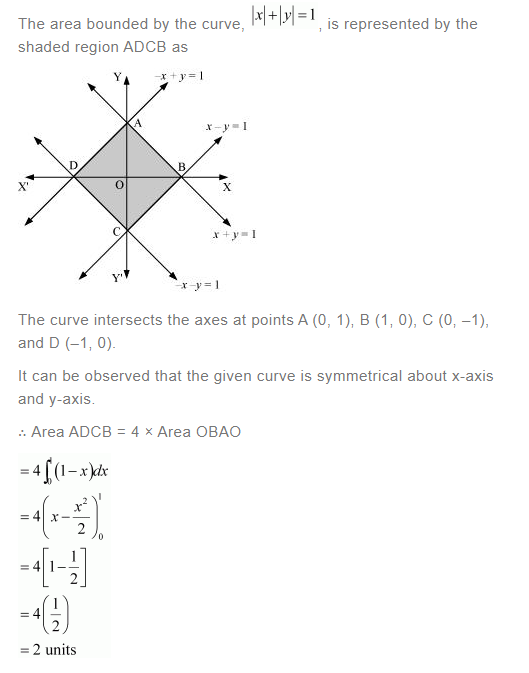
Question 11:
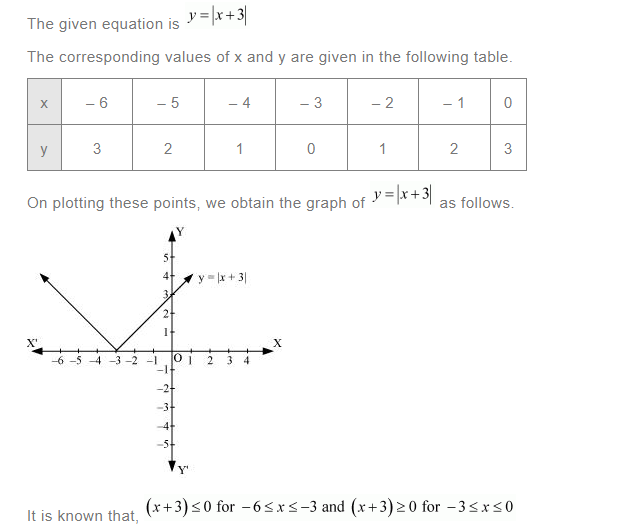
[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]
Answer:
Question 12:
Answer:
Question 13:
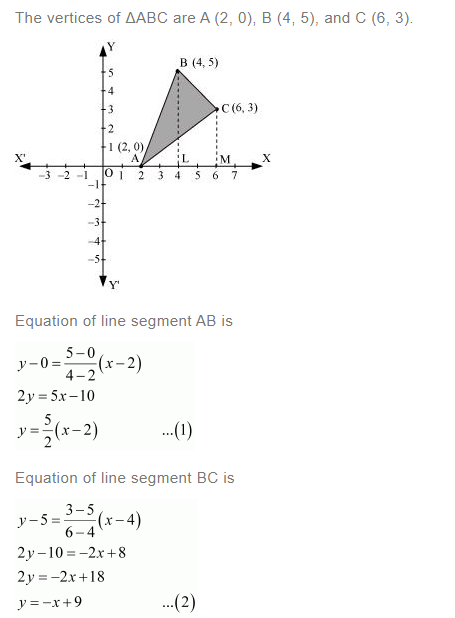
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A (2, 0), B (4, 5), and C (6, 3)
Answer:
Question 14:
Using the method of integration find the area of the region bounded by lines:
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Answer:
Question 15:
Answer:
Question 16:
Answer:
Question 17:
Answer:
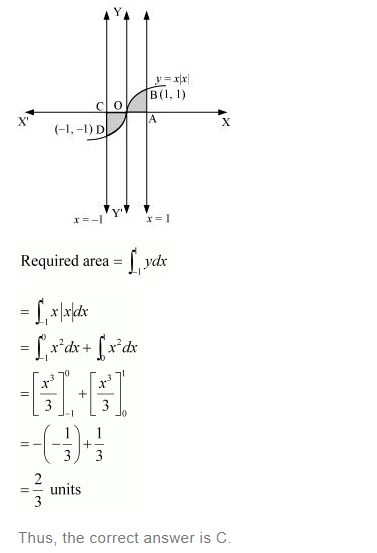
Question 18:
Answer:
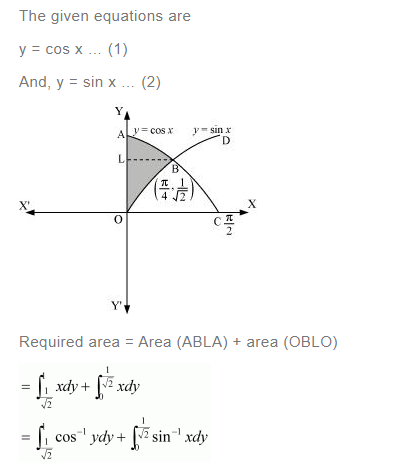
Question 19:
Answer: